Quina acció fa aquesta icona?... i altres preguntes

Ara que el curs ja està molt avançat, dediquem aquesta pràctica, que en gairebé tots els aspectes es pot considerar d'ampliació, a comentar "petites coses" (o no tan petites!) que no han aparegut al llarg de les pràctiques i que interessa que estiguin consignades en algun lloc del material del curs.

En concret parlarem de tres icones (Compàs, Inversió, Polar o diàmetre) i d'algunes possibilitats per a la representació de corbes que poden ser d'utilitat en l'aplicació del GeoGebra a la física o la tecnologia.

Sovint diem que en les obres cabdals de la geometria grega, amb els Elements d'Euclides en un lloc preeminent, les construccions es feien amb regle i compàs. En cap moment, en el context de les construccions clàssiques, apareix la noció de distància expressada numèricament.¹⁾

En canvi, en el GeoGebra hem treballat gairebé sempre amb magnituds mesurades numèricament; els punts lliscants han estat per a nosaltres un company de viatge constant.

Doncs bé, en la nova versió del GeoGebra s'ha fet un homenatge a les construccions amb regle i compàs mitjançant l'eina Compàs, una de les possibilitats per dibuixar una circumferència.

• Quan s'activa aquesta eina ens diu que primer hem d'assenyalar un segment. Quan ho fem és com si haguéssim obert un compàs que traça una circumferència que té per radi la longitud del segment. Després anem movent la circumferència ja feta fins que marquem el centre, i ja tenim la circumferència que buscàvem.

El procediment per posar en un punt del pla un segment igual a un altre (que és essencialment el que es fa amb aquesta eina Compàs) és tan important per a totes les construccions dels Elements com ho és la proposició 2.²⁾

Euclides ho feia a partir de la Proposició 1, que construeix un triangle equilàter sobre un segment donat.³⁾ Com faríem ara nosaltres aquesta construcció⁴⁾ amb l'eina Compàs?

Vegeu que s'ha fet tot sense el concepte de la mesura numèrica!

Encara un altre homenatge a l'ínclit Euclides. Com farem un angle igual a un altre? ⁵⁾

És a dir, per resumir: l'eina compàs és un homenatge conceptual a la geometria sintètica o constructiva dels grans mestres clàssics.

Si llegiu amb atenció la definició anterior i diem O el punt fix (o centre d'inversió) i a² la constant ⁶⁾, quins són els punts A que queden fixos per la transformació?

Si ha de ser OA · OA = a² és clar que això es complirà si i només si OA = a. Tots els punts d'una circumferència de centre O i radi a són fixos en la inversió. Aquesta circumferència de punts fixos (dita circumferència d'autoinversió) caracteritza la transformació i és la que ens demana la icona de la Inversió: primer el punt del qual volem trobar la imatge, després aquesta circumferència de punts fixos.

• Imagineu que la circumferència d'autoinversió és la de centre l'origen de coordenades i radi 4, és a dir x² + y² = 16. La constant de la inversió serà 16 i el centre d'inversió el (0,0).
• En quin punt es transformarà el punt (8,0)? Segur que pensant una mica deduïu que la resposta és el (2,0). Comproveu-ho amb el GeoGebra!
• En quin punt es transformarà el (0,2)? En el (0,8), és clar!
• I el punt (-4,4)? Si ho feu amb el GeoGebra veureu que té per imatge (-2,2). Raoneu que, efectivament, es compleix la definició.

En aquesta transformació es compleix que:

• Una recta que passa pel centre de la inversió es transforma en ella mateixa. És clar a partir de la definició.
• Una circumferència que no passa pel centre es transforma en una altra circumferència. Sabríeu veure-ho amb el GeoGebra? No es pot fer directament, la icona de la inversió només ens dóna la imatge d'un punt. Però sí que es pot fer amb el locus o lloc geomètric.
  • Suposem que ja tenim definida la circumferència c d'autoinversió.
  • Dibuixeu una altra circumferència. Podeu fer-ho amb circumferència donats el centre i un punt per on passa.
  • Situeu un punt nou, D sobre aquesta circumferència.⁷⁾
  • Feu el punt D', imatge de D per la inversió.
  • Feu el lloc geomètric de D' quan es mou D.
  • Veureu que efectivament és una circumferència. Creieu que el centre d'aquesta circumferència és el transformat per la inversió del centre de la circumferència original?
• Ara, la característica important de la inversió, que il·lustrarem amb una activitat GeoGebra.
  • Una recta que no passa pel centre d'inversió es transforma en una circumferència que passa pel centre d'inversió.
  • Una circumferència que passa pel centre d'inversió es transforma en una recta que no passa pel centre d'inversió.
• La inversió és una transformació que conserva angles i tangències, i per això té aplicació en la resolució constructiva de determinats problemes de geometria.⁸⁾ La idea seria la següent:
  • Un problema de tangències amb circumferències no el sabem fer.
  • Apliquem una inversió i les circumferències es transformen en rectes.
  • Resolem el problema de tangències amb les rectes.
  • Desfem la inversió (és a dir, tornem a aplicar la inversió, que és una transformació involutiva) i ja tenim la solució del problema.

Podeu llegir el text següent⁹⁾:

Tothom sap que en la geometria euclidiana una recta es fa amb un regle! Però un regle és una eina imperfecta, perquè s'ha de fer amb un altre regle; una circumferència, en canvi, no necessita una altra circumferència per a ser produïda, mai fem una circumferència resseguint una peça rodona. Per això el problema del traçat d'una recta a partir només d'una circumferència es va plantejar i es va resoldre entre els segles XVIII i XIX.
Des d’un punt de vista pràctic, això equival a la conversió d’un moviment circular en rectilini, que era imprescindible per a l’aplicació de les màquines de vapor: per això la primera solució (aproximada) al problema es deu al mateix Watt, que va inventar la màquina de vapor.
El problema no va ser resolt exactament fins a Peaucellier, i així va obtenir, de passada, un mecanisme que realitzava inversions.

Podeu trobar informació detallada sobre aquest mecanisme si poseu Peaucellier al Google. Per exemple, trobareu un article The Peaucellier-Lipkin linkage a la wikipèdia en anglès (en aquest cas, excel·lent informació) on veureu un esquema animat del funcionament del mecanisme. Us animeu a fer-lo amb el GeoGebra?

Practiqueu amb l'activitat següent, que ja veureu que és ben senzilla d'elaborar.

• Cliqueu primer de tot al botó de baix a l'esquerra per tal d'engegar l'animació i podreu observar la Visualització automàtica de la transformació d'un punt A que es mou sobre un segment.
• Observareu clarament la transformació d'un moviment rectilini en circular. Naturalment, de manera mecànica no es pot fer que un punt es mogui sobre "tota" una recta. Però conceptualment, sí!
• Quan us sembli oportú, pareu l'animació i cliqueu a la casella de verificació Visualització manual… i seguiu observant què passa, ara, quan es mou el punt P.¹⁰⁾ Quan us sembli oportú, feu el que diu la segona part de la casella de verificació …i lloc geomètric. Activeu l'eina Lloc geomètric i feu el lloc geomètric de P' quan es mou P…
  • … i com que el punt P està definit com un punt de la recta, no solament del segment, veureu que es completa el lloc geomètric: una circumferència!
• Podeu canviar el segment inicial i tornar a fer l'activitat
  

• Construïu una circumferència c, que serà la circumferència d'autoinversió. Convé que n'estigui a la vista el centre, que en l'activitat que heu vist hem batejat com punt O.¹¹⁾

Per a la primera part, la que pot funcionar automàticament:

• Definiu un segment donats per dos punts B i C.
• Definiu un punt lliscant k:
  • que variï de 0 a 1 amb increment 0.001,
  • com a característiques de l'animació podeu posar velocitat 4, i que la repetició sigui Oscil·lant.
• Definiu el punt A = B + k*(C-B) que, a mesura que va variant el punt lliscant k, recorre tots els punts del segment BC.
• Activeu la icona de la Inversió i marqueu primer el punt A i després la circumferència c. Així obtindreu el punt A'. Activeu-ne el traç.

I ja podeu mirar si tot funciona!

Per a la segona part, la que funciona manualment:

• Feu que es dibuixi la recta que passa pels punts B i C, que ja teniu definits.
• Definiu un punt P sobre la recta BC. Amb atenció que sigui sobre la recta i no solament sobre el segment BC.
• Activeu la icona de la Inversió i marqueu primer el punt P i després la circumferència c. Així obtindreu el punt P', que acolorireu igual que l' A'. Activeu-ne el traç.
• Així ja esteu a punt de fer el lloc geomètric de P' quan es mou P i, com ja heu vist en l'experimentació, comprovar que apareix una circumferència.

Ànim i guardeu la feina!

Si volem dibuixar una corba que té com a expressió en coordenades paramètriques
      x = x(t), y = y(t)       definida per a ≤ t ≤ b,
podem dibuixar-la amb la comanda següent:       corba[ x(t), y(t), t, a, b],
amb el benentès que:

• Si li voleu donar nom caldrà que escriviu, per exemple c = corba[ x(t), y(t), t, a, b] i el propi programa ja l'escriu a la finestra algebraica com c(t); no podem definir-la nosaltres directament com c(t).
• Les expressions de x(t) i y(t) han d'anar a dintre del comandament corba, no poden estar definides a part.
• Sí que es poden fer servir a la definició altres variables definides a fora del comandament, per exemple per un punt lliscant.
• t és simplement el nom del paràmetre, que pot ser qualsevol lletra.
• a i b són valors numèrics que, com és d'esperar, poden venir donats com a variables numèriques.

Teniu una bona font d'exemples en les corbes de Lissajous:     x = sin(w₁t), y = sin(w₂t + d) definides en l'interval 0 ≤ t ≤ 2π

• Feu proves per diferents valors dels paràmetres que intervenen: w₁, w₂, d, que podeu tenir definides per uns punts lliscants.

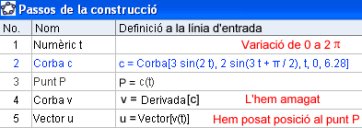
Una vegada definida una corba com c(t) podeu saber quin punt P correspon a cada valor del paràmetre.

• Si ho voleu saber per a un valor concret del paràmetre t = t₀, caldrà escriure a la finestra d'entrada P = c(t_0).
• Però ho podeu fer amb un punt lliscant que doni els valors del paràmetre… i aquest punt lliscant pot venir definit per la mateixa lletra que té el paràmetre dintre del comandament corba, i aleshores, si t és aquest valor numèric variable donat per un punt lliscant, c(t) ens mostra en cada moment el punt de la corba.
• Com que les corbes en paramètriques s'estudien a fons per al moviment dels cossos en un pla, apliqueu això que acabem de comentar juntament amb l'animació dels punts lliscants pot materialitzar el moviment. Vegeu-ho a la finestra següent assenyalant la casella de verificació corresponent.
• I, ja que parlem del moviment, podríem dibuixar el vector velocitat? Sí! També ho podeu comprovar.

Com s'ha fet l'activitat? A part del disseny de les caselles de verificació, que ja deixem per a les persones que feu el curs, així:

Si us interessa el tema podeu provar de…

• fer la tangent en el punt P de la corba (amb la icona de Tangents que teniu al grup d'icones de rectes, o també amb el comandament Tangent[P, c]),¹²⁾
• buscar el CercleOsculador[P, c] i relacionar-hi la Curvatura[P, c]

…i veureu que és ben cert el que dèiem suara: que podem treballar a fons amb les corbes donades en paramètriques.

Podem aprofitar la idea de la representació de corbes en paramètriques per transformar-hi una corba donada en coordenades polars i fer-ne la gràfica.

• Si l'equació en coordenades polars d'una corba és r = r(α), podem obtenir-ne una representació en paramètriques fent servir α, 0 ≤ α ≤ 2π com a paràmetre.
• Efectivament, sabem que és x = r · cos(α), y = r · sin(α).
• Haurem d'escriure això en l'expressió de la corba, amb el benentès que no podem tenir prèviament definida l'expressió de r com a funció de α i aprofitar-la a dintre de la definició de corba[ ], sinó que haurem d'escriure l'expressió per a la coordenada x i una altra vegada per a la coordenada y.

Alguns exemples:

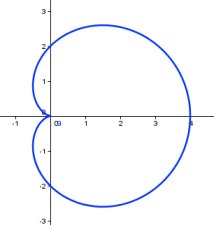
• La corba que en coordenades polars té l'expressió r = a (1 - cos(α)), és la cardioide. El valor de a dóna la mida de la figura.
  • Escriviu a la línia d'entrada corba[ 2 (1 - cos(α)) cos(α), 2 (1 - cos(α)) sin(α), α, 0, 2 π] i observeu:

• L'equació general, en coordenades polars r = r(α), de les còniques del pla és 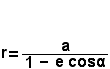, on a és un paràmetre que dóna la grandària de la cònica i e és l'excentricitat.
  • Podeu definir dos punts lliscants a i e, que podeu fer variar cada un de 0 a 4, i representar la corba com s'ha indicat.
  • Comproveu que la gràfica de l'equació anterior si 0 < e < 1 es tracta d'una el·lipse, si e = 1, una paràbola, i si e > 1, una hipèrbola.
• Finalment, si poseu r = a cos(5 α), obtindreu una rosassa de 5 fulls, tant més gran segons el valor que vulgueu donar a la a.

Aquesta pregunta no té una resposta tan clara com les anteriors i entrem en un tema que no apareix, ni de lluny, en els currículums de Secundària. Tanmateix, hem cregut oportú fer-hi una breu referència; potser aquest apartat us pot suggerir un bon tema per al treball final.

Entrem en el camp de la la geometria mètrica on tenen una importància cabdal la proporcionalitat de segments amb la invariància de la raó simple per projecció paral·lela (que hem vist amb el Teorema de Tales i que s''empra en els teoremes de Menelao i de Ceva) i el concepte de quaternes harmòniques i la invariància projectiva de la raó doble, que ens porta a la definició de pol i polar respecte a una cònica.¹³⁾

• Comentarem algunes propietats que compleix la recta polar d'un punt respecte a una cònica; moltes d'elles es troben com a definicions segons el context i les altres se'n dedueixen.
• Dibuixar la recta polar d'un punt relativa a una cònica no té cap dificultat amb la icona corresponent. L'ajuda de la barra d'eines ens ho indica clarament: Primer el punt… després la cònica.
• Habitualment el pas d'un punt a la seva polar té un tractament dual exacte, en el pas d'una recta al seu pol, però no és així en el GeoGebra.

Tot i que enunciarem algunes propietats des d'un punt de vista descriptiu, ho farem amb la idea posada en el fet que el GeoGebra ens permetrà comprovar empíricament, d'una manera ben elegant, cada propietat, en molts casos amb l'ajut de la comanda locus o lloc geomètric i amb la visió gràfica que ens facilita el GeoGebra. No ens interessa en aquest moment aprofundir en els temes de la geometria algebraica sinó, ara que ja acabem el curs, insistir en la potència per a conjecturar i mostrar propietats que ens ofereix el treball amb el GeoGebra.

• El fet que ja hem esmentat de la invariància de la raó doble per les projectivitats fa que aquesta sigui una idea clau en la geometria projectiva.

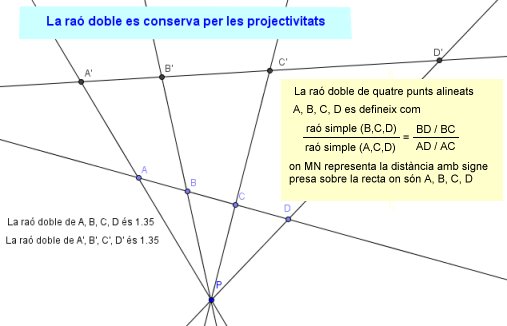
• Podeu fer la construcció anterior sense cap problema.
  • Dibuixeu un punt P. Dibuixeu una recta i sobre ella quatre punts A, B, C, D. Dibuixeu una altra recta. Feu la projecció des de P sobre aquesta recta dels punts A, B, C, D. Podeu constatar la conservació de la raó doble amb la comanda de GeoGebra RaóDoble[A, B, C, D].

• Es diu que quatre punts alineats A, C, B, D (em aquest ordre) formen una quaterna harmònica, o també que el parell (A, B) és conjugat harmònic del parell (C, D) si el resultat de RaóDoble[A, C, B, D] és −1.

• Donat un punt A i una cònica c es pot considerar el conjunt de tots els punts B amb la propietat que si X, Y són els punts d'intersecció de la recta AB amb la cònica, aleshores la quaterna A, X, B, Y és una quaterna harmònica. Es demostra que aquest lloc geomètric és una recta r que rep el nom de recta polar d'A respecte a c.
• Recíprocament, A rep el nom de pol de r respecte a c.
  • Podeu comprovar-ho amb el GeoGebra. Dibuixeu una cònica c i un punt A. Amb la icona corresponent feu la polar de A respecte c. Traceu una recta qualsevol que passi per A i feu que el punt B sigui la intersecció d'aquesta recta amb la polar i que els punts X, Y siguin les interseccions de la recta amb la cònica C. Observareu que, sempre, RaóDoble[A,X,B,Y]=-1.

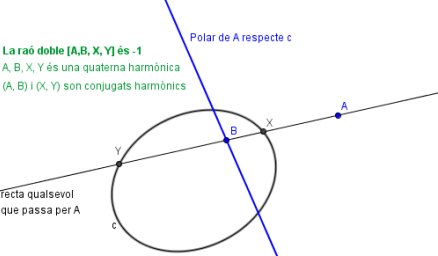
• Propietats que podeu comprovar amb construccions de GeoGebra.
  • Si A és un punt des del qual podem traçar dues tangents a una cònica c (per exemple un punt exterior a un a el·lipse), aleshores la recta polar de A respecte c passa pels dos punts de tangència.
  • Una altra propietat molt important:
    
    
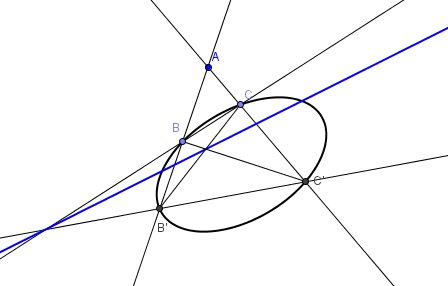
    • Dibuixeu una el·lipse i un punt A exterior a l'el·lipse.
    • Situeu dos punts B i C sobre l'el·lipse.
    • Busqueu els punts B' i C' d'intersecció amb la cònica de les rectes AB i AC.
    • El punt d'intersecció de la recta BC amb la recta B'C' és un punt de la polar de A respecte de la cònica.
    • El punt d'intersecció de la recta BC' amb la recta B'C és un altre punt de la polar…
    • …i coneguts dos punts de la polar, ja la podem dibuixar.
  • Observeu que aquesta propietat (que és vàlida per a totes les còniques, no solament per a l'el·lipse), combinada amb l'anterior, ens permet traçar les tangents a una cònica només amb un regle: es fa la polar pel procediment que indica la darrera propietat i com que sabem que els punts d'intersecció de la polar amb la cònica són els punts de tangència… ja hem acabat!
  • Assageu de trobar alguna propietat que es compleixi per a un punt A i la recta polar d'A respecte de c si A és un punt des del qual no es poden traçar tangents a una cònica c (punt interior en el cas d'una el·lipse).

Per acabar comentarem quina propietat té la recta que ens retorna la icona Polar o diàmetre si entrem com a primer argument una recta.¹⁴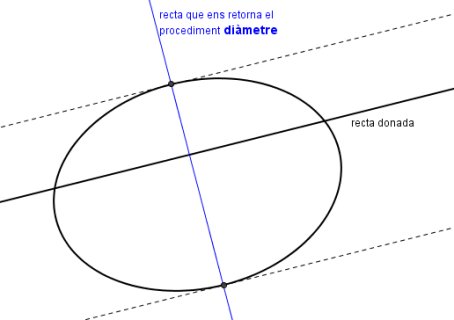⁾ Segur que amb la figura anterior, que construireu sense cap dificultat amb el GeoGebra per veure'n la generalitat, veieu la propietat que volem enunciar:

• Les tangents a l'el·lipse pels punts on el diàmetre que ens retorna l'eina Polar o diàmetre talla l'el·lipse són paral·leles a la recta donada.
• Dos diàmetres d'una el·lipse es diuen diàmetres conjugats, si un diàmetre és paral·lel a la tangent de l'el·lipse per l'extrem de l'altre diàmetre i viceversa.
  • Si penseu una mica, veureu de seguida que la icona Polar o diàmetre ens permet trobar parelles de diàmetres conjugats.
  • Els únics diàmetres conjugats ortogonals d'una el·lipse són els seus eixos.

És clar que en el temps destinat al curs no podem parlar de totes les possibilitats del GeoGebra. Amb aquest apràctica n'hem volgut comentar algunes per si a algú li poden interessar!