La tangent a una corba i la funció derivada
En aquesta pràctica veureu que les comandes Tangent i Pendent representen una manera molt àgil de visualitzar la definició de la derivada d'una funció en un punt.
S'aprofitarà aquest recurs per generalitzar el càlcul per a tots els punts, i així es generarà punt a punt la gràfica de la funció derivada.
La pràctica acaba amb dues propostes d'ampliació.
La funció derivada
Observeu el funcionament de l'activitat següent, movent el punt A sobre l'eix de les x.
En aquest cas, per fer la construcció deixeu visibles els eixos i invisibles la finestra algebraica i la graella.
- Entreu la fórmula de la funció que farem servir per treballar el concepte de funció derivada: f(x) = x³/9 - x² /2 + 3 (És clar que podeu entrar a qualsevol altra!).
- Per evitar moviments accidentals d'aquesta gràfica, feu clic damunt amb el botó dret del ratolí i accedint a Propietats activeu l'opció Fixa objecte. D'aquesta manera, aquesta gràfica restarà fixa.
- Amb l'eina Punt nou definiu un punt A sobre l'eix d'abscisses i, per simplificar la notació posterior, entreu a=x(A).
- Definiu el punt B=(a,f(a)) que quedarà situat sobre la gràfica.
- Entreu la comanda tangent[B,f]. Observeu que s'ha dibuixat, directament, la recta tangent a la gràfica de f(x) que passa per B. En la pràctica anterior dibuixàvem la tangent mitjançant l'eina incorporada als menús; ara veiem que podem dibuixar automàticament la tangent també amb una comanda. Encara tenim una altra manera: escrivint-ne l'equació on es posa de manifest que el seu pendent és la derivada en el punt. Quan ja tingueu la recta tangent dibuixada li podríeu canviar el nom i batejar-la com t.
- Entreu la comanda p = Pendent[t]. Observeu que s'ha dibuixat un triangle petit que ens indica el pendent de la recta tangent a la corba en el punt B.
- Moveu el punt A i observeu la manera com la tangent i el pendent van variant.
- Dibuixeu el segment AB i feu que es vegi amb una línia discontínua.
A continuació definireu un punt P que servirà per construir la funció derivada.
- Entreu la definició P = (a, p), on convé recordar que a és la primera coordenada del punt A i p és el pendent de la recta tangent en A. Ja veieu que estem considerant, per a cada abscissa, la corresponent derivada de la funció.
- Cliqueu amb el botó dret del ratolí sobre el punt P i accediu a l'opció Propietats. Ara, podeu canviar el color del punt i, sobretot, heu d'activar l'opció Activa el traç. D'aquesta manera quan el punt B es mogui, deixarà marcada la traça, que serà la funció derivada.
Activeu el mode Mou, desplaceu el punt A i observeu què es va dibuixant. És la funció derivada? És clar que sí, però per comprovar-ho podeu fer això:
- Entreu la comanda f'(x). Observareu que s'ha creat a la finestra algebraica la funció g(x), que és la derivada de la funció f(x). També ja es veu la gràfica de g(x), és a dir, de f'(x). Fent clic sobre aquesta gràfica amb el botó dret podeu accedir a Propietats i canviar-ne el color.
- Potser pensareu que és interessant, per a l'ús didàctic, que la gràfica de la funció derivada no es vegi permanentment. Ànim, doncs. Ja sabeu que només cal que creeu una casella de verificació que ho permeti!
Desplaceu el punt A i observeu com la traçada del punt coincideix amb la gràfica de la funció derivada.
Per esborrar la traçada podeu prémer Ctrl-F o bé accedir a Visualitza | Actualitza (cosa que també, quan s'ha guardat l'activitat en una pàgina web, podeu fer amb la icona d'actualitzar que es pot fer aparèixer a la finestra interactiva).
Canvieu d'acord amb les vostres preferències el color i l'aspecte dels objectes que hi apareixen. I no us oblideu de guardar la feina!
Dues propostes d'ampliació
En aquest apartat teniu dues propostes que tal vegada us podran servir per algun treball de recerca, o bé si teniu l'ocasió de fer una optativa d'ampliació de matemàtiques a segon de Batxillerat o, simplement, com a element de reflexió sobre la potència de GeoGebra.
Visualització del mètode de Newton de resolució aproximada d'equacions
A la Wikipèdia llegim: En càlcul numèric, el mètode de Newton, o mètode de Newton-Raphson1) és un algoritme per tal de trobar aproximacions del zero d'una funció amb valors reals.
Com que aquest és el mètode que acostuma a ser més eficient per calcular solucions aproximades d'equacions, tot fa pensar que és el que porta incorporat el GeoGebra. Per altra banda, com que és un mètode iteratiu ens servirà per explicar la possibilitat d'emprar una macro i per visualitzar les successives aproximacions.
Llegim una mica més la Wikipèdia: Per aplicar el mètode de Newton s'escull un valor de l'abscissa raonablement pròxim a l'autèntic zero (llavor). Es busca el punt corresponent de la gràfica de la funció i, en aquest punt, es reemplaça la corba per la seva tangent, i es calcula el zero d'aquesta recta tangent. Aquest zero, normalment, és més pròxim al zero de la funció que el valor inicial. Aquest procés es reitera, fins arribar a una aproximació que es dóna per bona.
Per seguir fil per randa l'aproximació anterior i fer una iteració del mètode de Newton:
- Entreu una funció de la qual voleu trobar un zero aproximat.
- Definiu un punt A sobre l'eix d'abscisses.
- Traceu per A una recta perpendicular a l'eix d'abscisses.
- Amb l'eina Intersecció de dos objectes busqueu el punt d'intersecció d'aquesta recta amb la gràfica de la funció. Serà el punt B.
- Entreu Tangent[B, f] i ja estarà dibuixada la tangent.
- Busqueu la intersecció d'aquesta recta tangent amb l'eix de les x. Aquest serà el valor que ens dóna la primera iteració del mètode prenent com a llavor l'abscissa del punt A.
Si ho heu fet 2), tindreu quelcom semblant a això:
Aquí ja hi teniu definida una eina (macro) per visualitzar successives iteracions del mètode.
- Per experimentar, activeu l'eina newton al grup d'eines creades per l'usuari. Ja veureu que us demana una funció i un punt. Cliqueu sobre la gràfica de la funció i al punt C i tindreu la segona iteració. Cliqueu sobre la funció i el punt de l'eix x que us n'ha resultat i tindreu una nova aproximació. I així successivament!
- Podeu moure el punt que ens dóna la llavor i veureu com evolucionen els resultats del mètode. Segurament constatareu que si prenem un valor inicial a prop del mínim costa més que el mètode convergeixi.
Per crear la macro, què hem fet?
- Hem anat a Eines / Crea una eina nova
- Com a objectes de sortida hem triat (amb la notació de les indicacions que es donaven abans) el punt C, el punt B i les dues rectes dibuixades (la recta vertical per trobar el punt de la corba i la tangent).
- Com a objectes d'entrada, a part de la funció f que com és lògic ja està posada per defecte, hem triat el punt A.
- Finalment li hem donat a la nostra nova eina el nom de newton i ja és a punt de funcionar.
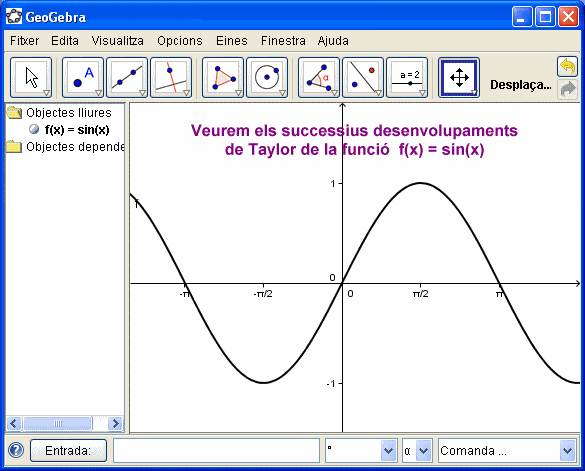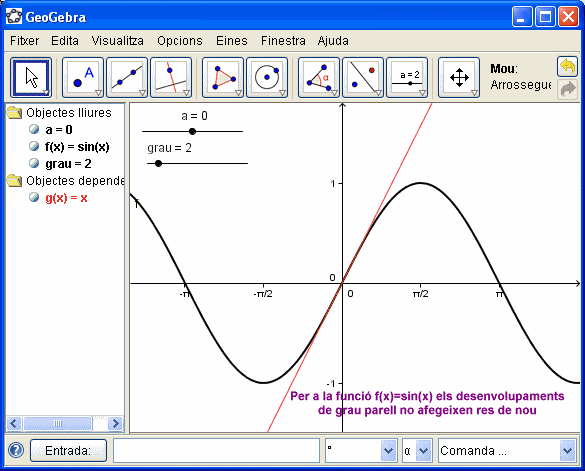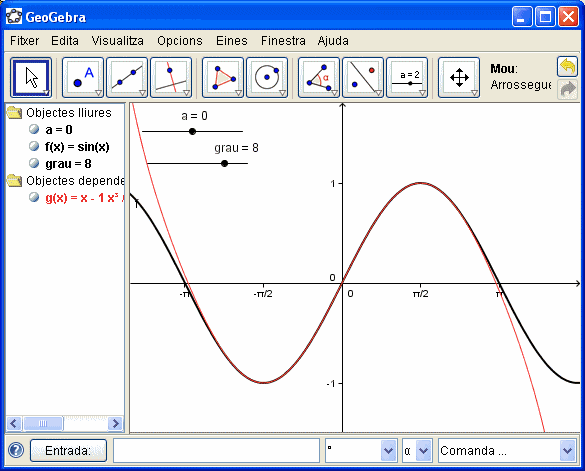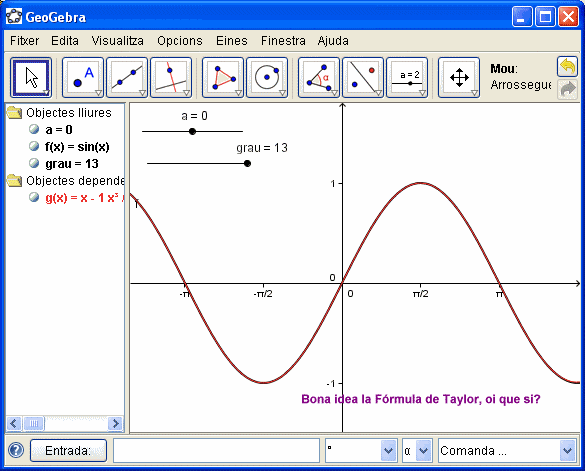
Visualització de l'aproximació de Taylor d'una funció
- En aquest cas us donem, sense més comentari que allò d'"una imatge val més que mil paraules" una successió de pantalles de GeoGebra que il·lustren l'aproximació d'una funció mitjançant el polinomi de Taylor.
Cliqueu aquí si us interessa el tema
- Ben segur que, a aquestes alçades del curs, si mireu amb atenció l'animació anterior, podreu elaborar ràpidament l'activitat interactiva que les ha generat. Ànim amb la feina!

