Una mica de programació lineal (*)

En un curs d'introducció al GeoGebra com el que esteu acabant, és impossible il·lustrar totes les possibilitats del programa, que només acabareu de conèixer després d'una investigació personal llarga i constant. Als Fòrums d'usuaris, o buscant altres pàgines amb activitats del GeoGebra, veureu propostes molt i molt interessants.

En aquesta pràctica es donen algunes idees per a un treball visual que pot ajudar a presentar el tema de la programació lineal.

Una inequació amb dues variables

En la pantalla següent del GeoGebra podeu experimentar per tal de fer visual que una recta ax + by = c divideix en pla en dos semiplans que –incloent en cada un la recta– són les solucions de les inequacions ax + by ≥ c i ax + by ≤ c.

Moveu el punt A i observeu.
Canvieu els valors dels coeficients que defineixen la recta i observeu.

Disculpeu, l'applet del Geogebra no es pot iniciar. Si us plau, assegureu-vos de tenir instal·lada la versió 1.4.2 o superior de la màquina virtual del Java. (Feu clic per començar ara la instal·lació)

Construcció

Per tal de poder moure-us, quan us interessi, exactament a punts sobre una recta de coeficients enters, és convenient que feu que la graella sigui visible i que Opcions|Enganxar els punts a la graella estigui actiu.

Definició de la recta:

De la manera que ja sabeu a bastament, definiu tres punts lliscants a, b i c que han de representar els coeficients de la recta ax + by = c. Poseu-hi els intervals de variació i l'increment que us semblin més adients. Suggerim increment 1 per treballar amb nombres enters.
Escriviu a la finestra d'entrada de comandes ax + by = c i ja tindreu la recta dibuixada. Doneu-li el nom R. Accediu al quadre de propietats de la recta, doneu-li la presentació que us interessi i feu que al desplegable de Mostra etiqueta aparegui Valor.

Punt mòbil i rètol que indica quina inequació es compleix:

Amb l'eina Punt nou definiu un punt A, que serà el que mourem per visualitzar experimentalment quin és el conjunt de solucions d'una inequació.
Definiu un valor numèric m = a*x(A) + b*y(A).¹⁾
Perquè el rètol que es comenta seguidament s'escrigui de manera correcta, i evitar així que apareguin expressions del tipus 4 x + - 5 y = 3, s'ha tingut en compte de diferenciar la situació en què b és positiu d'aquella en què b és negatiu.
- Amb l'eina Insereix text definiu un text així:²⁾

 Si[b≥0, a+"x+"+b+"y ="+m+" > "+c, a+"x"+b+"y ="+m+" > "+c]

que apareixerà en el punt de la pantalla on hàgiu clicat i mostrarà quelcom semblant a:
.
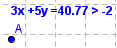Accediu a la finestra de Propietats d'aquest text, doneu-li les característiques tipogràfiques que us interessin, clicant a la pestanya Posició associeu-lo al punt A³⁾ i, finalment, clicant a la pestanya Avançat poseu com a condició perquè es vegi l'objecte la següent: a*x(A) + b*y(A) > c .

Feu semblantment amb un text anàleg (associat també al punt A), perquè ara es vegi un text una mica més curt, com és ara:

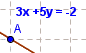
Caldrà canviar el signe > per = en el text i no repetir, així

 Si[b≥0, a+"x+"+b+"y = "+c, a+"x"+b+"y ="+c]

. Feu que la condició sigui, en aquest cas, a*x(A) + b*y(A) ≟ c.

I una altra vegada amb un text semblant, però amb < (tant en el text com en la condició).

Falta, finalment, acolorir el semiplà en què es compleix ax + by > c. Tanmateix, amb el GeoGebra no es poden definir semiplans i el que farem serà definir un rectangle "molt gran" que "imitarà" el semiplà.⁴⁾

Considereu un punt sobre la recta. Podeu fer-ho amb l'eina Punt nou o, potser preferiblement en aquest cas, definint B=Punt[R]. Feu que no es mostri.
Definiu ara dos vectors: v=(-100b, 100a) i w=(100 a, 100b)⁵⁾, que són, respectivament, un vector "gran" director de la recta i un vector "gran" perpendicular a la recta que va cap al semiplà positiu.
Definiu ara P = B+v, P1 = P+w, Q = B-v i Q1 = Q+w. Seleccioneu tots aquests punts alhora i feu que no es mostrin.
Definiu el polígon ombra = Polígon[P,P1,Q1,Q]. Ja s'haurà acolorit el semiplà positiu!
A la finestra algebraica hauran quedat definits també els quatre segments que són els costats d'aquest polígon. Seleccioneu-los tots quatre alhora i feu que no es mostrin els corresponents objectes.

Guardeu la feina i, si us animeu, practiqueu-ho repetidament per elaborar l'activitat següent.

La regió factible i la funció objectiu

Tot seguit teniu una proposta que repeteix per tres funcions la feina que acabem de mostrar i divideix el pla en regions. ⁶⁾

Per cada regió s'indica amb un punt mòbil A quin és el sistema d'inequacions del qual aquella zona és la regió factible.

També s'han entrat els coeficients de la funció objectiu (definida de manera anàloga a les anteriors) i es mostra el valor que pren en el punt mòbil, i així es pot veure empíricament que els valors extrems s'assoleixen en els vèrtexs.

Disculpeu, l'applet del Geogebra no es pot iniciar. Si us plau, assegureu-vos de tenir instal·lada la versió 1.4.2 o superior de la màquina virtual del Java. (Feu clic per començar ara la instal·lació)

Estudieu aquesta activitat i, si escau, pregunteu dubtes!

¹⁾ Tot i que el GeoGebra admet l'espai en blanc com a signe de producte, i així presenta el programa les expressions formals, ens ha semblat molt més clar, tipogràficament, indicar-ho amb el signe de producte, que és l'asterisc.

²⁾ Recordeu, com sempre, que entre les " " hi va el text que volem que aparegui, i que "fora de les cometes" hi indiquem els valors numèrics que volem que vagin canviant.

³⁾ Com ja sabeu, després el podeu moure a mà perquè es vegi millor i aquest petit desplaçament s'enregistra.

⁴⁾ Si en algun cas es vol aprofitar aquesta pràctica per treballar amb coeficients molt grans, tal vegada convindrà modificar algun valor en la construcció que s'explica.

⁵⁾ Convé recordar que si a la finestra de comandes entrem una variable en majúscula =(..,..), el GeoGebra considera que es tracta d'un punt; i si fem una variable en minúscula = (.., ..) es crea un vector.

⁶⁾ En comptes d'entrar els coeficients de les funcions amb punts mòbils, que farien que no es veiés res al gràfic, els entrem directament a la finestra algebraica. Però recordeu que, fent-ho així, aleshores si seleccioneu un d'aquests punts també podeu modificar-ne el valor amb les Fletxes de cursor.