Concepte d'integral i càlcul d'àrees. La distribució normal

Si consultem l'ajuda del programa GeoGebra pel que fa a les integrals, trobarem tres entrades que han permès compondre la imatge següent:

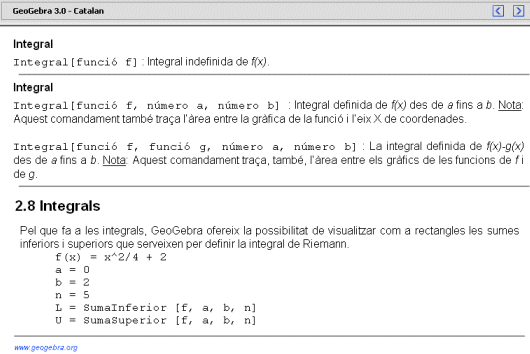
En aquesta pràctica experimentarem amb aquestes comandes i observarem l'excel·lent informació gràfica que ens dóna GeoGebra quan apliquem la comanda Integral[ ].

Primer de tot veureu que és molt ràpid elaborar una activitat en què es constata visualment què és el que es calcula quan es troba el valor d'una integral definida i, en canvi, què cal considerar per calcular l'àrea entre una corba, l'eix de les x i les rectes x=a i x=b en el cas que hi hagi diferents zones en l'àrea per calcular. Deixarem com a proposta per als exercicis el càlcul i la visualització de l'àrea entre dues corbes.

Continuarem amb una presentació que ajudarà, sens dubte, en les nostres classes d'introducció al concepte d'integral. Constatarem novament que els recursos de GeoGebra ens ajuden molt i molt.

Finalment es comentarà el fet que hi ha incorporats al programa recursos per al càlcul numèric d'integrals, que es concretaran en la situació d'aplicació més repetida que necessita aquests recursos: l'estudi de la distribució normal.

Ja heu llegit que la comanda fonamental per al càlcul integral és Integral[ ].

• Amb un sol argument, Integral[f], es calcula una funció primitiva. ¹⁾
• Amb tres arguments, o amb quatre, es calculen integrals definides. L'explicació que dóna l'Ajuda és ben clara.

Comenceu per fer algunes pràctiques amb funcions diverses i veureu de seguida que, a part de fer els càlculs, la visió gràfica que incorpora la comanda és ben interessant.

• Quan es calcula una primitiva, encara que no estigui dibuixada la funció que integrem, es dibuixa sempre una funció integral.
• Quan es calcula una integral definida s'acoloreix la zona que correspon al càlcul realitzat.

Ja sabeu que, per a la definició de la funció integral les àrees que estan per sobre de l'eix d'abscisses es computen com a positives i les que estan per sota de l'eix es prenen negativament. Per això és interessant visualitzar, tot seguit, la diferència formal

A continuació es presenta una activitat per visualitzar què es calcula quan es fa la integral d'una funció entre x=a i x=b ²⁾ i diferenciar-ho ben clarament del càlcul del valor absolut de l'àrea.

• S'ha fet per a la funció f(x)=x²-4x+3, però (a part d'aspectes de presentació) no hi ha cap diferència per fer-ho amb una altra funció. Només caldrà canviar la funció a la finestra algebraica.
• Es calcula i es poden visualitzar, o no:
  • la integral des de x=a fins a x=b donats per punts lliscants, calculada amb la comanda integral = Integral[f, a, b],
  • el valor de l'àrea total de les zones tancades compreses entre la corba, l'eix de les x i les rectes x=a i x=b, que es calcula mitjançant la integral definida del valor absolut de la funció, és a dir amb la comanda àreacorba = Integral[ abs(f(x)), a, b].

Aquesta activitat permet observar molt clarament les diferències entre allò que es calcula en un cas i en l'altre. Comproveu-ho activant les caselles de verificació i observeu els resultats a la finestra algebraica.

Proveu d'elaborar personalment aquesta activitat. Segur que a aquestes alçades del curs reeixereu en l'intent. Tanmateix, consulteu tots els dubtes o anomalies que es presentin.

Però la comanda integral no és l'única de què disposa el programa, sinó que conseqüentment amb l'objectiu didàtic de la creació de GeoGebra (recordeu que porta com a subtítol Dinamic Mathematics for School) disposem d'eines que reforcen la presentació del concepte d'integral definida.

En l'aplicació que teniu a la finestra activa següent podeu calcular la suma superior i la suma inferior corresponents a uns determinats límits d'integració i nombre d'intervals. Podeu variar els límits d'integració³⁾ i, mitjançant un punt lliscant, el nombre d'intervals. Observeu en cada cas la variació de les sumes, la diferència entre la suma superior i inferior, i la convergència d'ambdues cap a un valor fix: la integral definida.

Per editar la funció i poder-la canviar, heu de fer doble clic sobre la seva expressió a la finestra algebraica.

Comentem tot seguit com es fa la construcció. Deixeu la finestra algebraica oberta.

• Entreu la funció f(x) = x³ - 2 x² + 4.
• Fixeu dos punts, A i B, sobre l'eix d'abscisses.
• Definiu un punt lliscant a, només amb valors naturals de l'1 al 200, i situeu-lo al lloc que es veu a la finestra anterior. Aquest punt lliscant controlarà el nombre d'intervals. Feu que inicialment agafi el valor 3.
• Definiu les sumes superiors entrant la comanda SumaSuperior[f, x(A),x(B),a]. Observeu que automàticament s'han dibuixat els rectangles corresponents al nombre d'intervals indicat per a i que a la finestra algebraica es calcula aquesta suma superior.
• Feu el mateix amb la suma inferior, entrant la comanda SumaInferior[f,x(A),x(B),a].
• Moveu el punt lliscant i els punts A i B i observeu els resultats.
• Entreu la comanda Integral[f,x(A),x(B)]. Aquesta és la integral definida de f(x) entre les primeres coordenades de A i de B. Observeu que el seu valor apareix a la finestra algebraica.

Segur que no tindreu cap problema per escriure els primers textos que apareixen per visualitzar la informació a la finestra gràfica (cas que vulgueu presentar l'activitat amb la finestra algebraica tancada). A continuació expliquem el darrer rètol.

• Per al rètol de la integral definida és necessari activar l'opció Fórmula LaTeX, recordar com es combinen textos fixos i valors variables i tenir en compte com es posa amb LaTeX un exponent (amb el ^) i com es posen subíndexs (amb _). Aleshores escriureu
  

"\int " + "_{" + a + "} ^{" + b + "} " + f + "  dx = " + c 

Ànim amb la feina! No us oblideu de guardar-la!

No us oblideu tampoc de fer algun exemple en el qual el valor de la funció en un dels extrems sigui negatiu i reflexionar bé, en aquest cas, sobre què representen la suma superior i la suma inferior.

Què succeeix si, en les activitats anteriors, definíssim com a funció f una funció de la qual no es pogués calcular la primitiva?

Tot funcionaria exactament igual que el que hem vist excepte, naturalment, el dibuix de la funció integral, que apareixeria com un objecte no definit.

Això és així perquè el GeoGebra incorpora mètodes numèrics per al càlcul de les integrals definides. Tot seguit en teniu un exemple amb la distribució normal.

• Podeu modificar els valors de la mitjana i la desviació estàndard seleccionant les variables μ o σ a la finestra algebraica. Això es pot fer tant entrant el nou valor a mà després de fer-hi doble clic, com amb les Fletxes de cursor una vegada tenim seleccionada la variable que interessi.⁴⁾
• Podeu variar els límits de l'interval del qual es calcula la probabilitat movent els punts que el defineixen sobre l'eix de les x.
• Podeu fer que es mostrin, o no, els intervals centrats en la mitjana μ i de radis respectius σ, 2σ i 3σ que ja sabeu que tenen molta importància en l'estudi de la distribució normal.

Construcció de la corba que dóna la distribució normal:

• Definiu a la finestra d'entrada de comandes i funcions els valors que us interessin per a les dues variables μ i σ⁵⁾ que donaran la mitjana i la desviació estàndard. Podeu fer servir lletres gregues amb el desplegable corresponent.
• Recordeu que la fórmula de la distribució normal és:
  

.
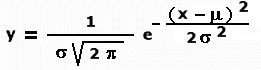Podeu definir, doncs, f(x)=exp(-(x-μ)²/(2σ²))/(σ*sqrt(2*pi)) i ja tindreu dibuixada la corba normal. Doneu-li els aspectes de presentació del vostre gust.

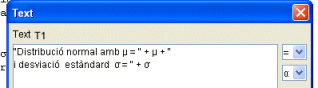
• Podeu fer un rètol que indiqui aquests valors i donar-li la presentació convenient.

Definició de l'interval i càlcul de la probabilitat com una integral definida.

• Amb l'eina Punt nou definiu dos punts A i B sobre l'eix de les x.
• Per simplificar l'escriptura posterior podeu definir ara dues variables a=x(A) i b=x(B), que són els valors que determinen l'interval del qual ens interessa calcular la probabilitat.
• La probabilitat que la distribució normal que estudieu prengui un valor entre a i b és Integral[f,a,b]. Entreu aquest valor amb el nom que vulgueu a la finestra d'entrada de comandes i funcions i ja tindreu calculada la probabilitat i dibuixada l'àrea que la representa. ⁶⁾
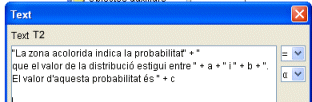
• També és interessant fer un rètol il·lustratiu adequat i situar-lo on interessi de la pantalla.

Finalment, per poder mostrar els punts μ-3σ, μ-2σ, μ-σ, μ-3σ, μ, μ+σ, μ+2σ, μ+3σ, ben interessants en l'estudi de la distribució normal, i situar-hi els rètols corresponents, fareu el següent:

• Definiu a la finestra d'entrada els punts (μ-3σ,0), (μ-2σ,0), (μ-σ,0), (μ-3σ,0), (μ,0), (μ+σ,0), (μ+2σ,0) i (μ+3σ,0).⁷⁾
• Seleccioneu tots aquests punts alhora i doneu-los els aspectes de presentació que us interessin.
• Escriviu cada un dels rètols μ-3σ, μ-2σ, μ-σ, μ-3σ, μ, μ+σ, μ+2σ, μ+3σ (amb el corresponent desplegable de lletres gregues). Col·loqueu cada un on escaigui. Seleccioneu-los tots alhora i acoloriu-los com us interessi.
• Per acabar, accediu a Edita | Propietats i associeu cada rètol al seu Punt origen. Acabeu de situar el rètol a mà.
• Creeu una Casella de verificació en la qual posareu els set punts i els set rètols que acabeu de crear. En la pràctica que s'ha presentat li hem posat el títol de Intervals però, naturalment, podeu posar-n'hi un altre que us sembli millor.

Guardeu la feina i practiqueu! No us oblideu de visualitzar en alguna ocasió la distribució normal estàndard i recordar i memoritzar quins són els valors de les probabilitats en els intervals [μ-3σ,μ+3σ], [μ-2σ,μ+2σ] i [μ-σ,μ+σ].