Aspectes locals de l'estudi de les funcions

En aquesta pràctica començarem amb una reflexió sobre el càlcul de derivades que incorpora el GeoGebra i ho aprofitarem després per mostrar com es pot visualitzar la relació entre el valor de la primera derivada d'una funció en un punt i la monotonia de la funció i, més en concret, amb els extrems de la funció. També és possible representar la segona derivada i relacionar-la amb la concavitat i la convexitat, però centrarem l'atenció, només, en els punts d'inflexió.

Càlcul de derivades

En la pràctica anterior ja s'ha posat de manifest que, donada una funció y = f(x), podíem obtenir la seva funció derivada escrivint, simplement f'(x). Aleshores el GeoGebra defineix una nova funció g(x) que és justament f'(x).

També és possible calcular la derivada en el punt corresponent a x=a entrant f'(a).

Semblantment podem obtenir la segona derivada escrivint f ''(x)(amb dos apòstrofs, no amb les cometes) i els valors de la segona derivada amb f ''(a); podem treballar amb la tercera derivada escrivint f '''(x) (amb tres apòstrofs), etc.

Els recursos de càlcul del GeoGebra són molt eficients i correctes, però, tanmateix, l'escriptura formal de les derivades no sempre és la que nosaltres mostraríem "a mà", i això succeeix especialment quan en la definició de les funcions apareixen paràmetres donats per punts lliscants.

És interessant comentar la comanda Derivada[].

Derivada[f] calcula la funció derivada de la funció f(x) i naturalment la dibuixa. Si ho feu així, a la finestra algebraica veureu f'(x) com a definició d'aquesta nova funció.
Derivada[f, n] calcula la derivada n-sima de la funció f(x), i també en aquest cas a la finestra algebraica veureu f ''(x), o f '''(x), etc., com a identificació d'aquesta nova funció.

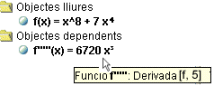
Ara bé, la comanda Derivada[] no permet calcular els valors de la derivada o de les derivades successives en un punt.

És clar, doncs, que en l'elaboració de les pràctiques els autors hem optat per una de les dues maneres de treballar, però també és clar que convé conèixer-les les dues i decidir en cada cas quina es fa servir.

Màxims, mínims i punts d'inflexió

Presentem tot seguit una activitat amb funcions polinòmiques per fer visuals els màxims i els mínims (extrems relatius) de la funció i de la derivada, i els punts d'inflexió de la funció per relacionar-los amb els extrems de la derivada. ¹⁾

Podeu definir una funció polinòmica de grau menor o igual que 4 amb cinc punts lliscants. Serà f(x) = a x⁴ + b x³ + c x² + d x + e i es visualitza la funció derivada i els màxims, mínims i punts d'inflexió. El resultat ha de ser semblant a:

Disculpeu, l'applet del Geogebra no es pot iniciar. Si us plau, assegureu-vos de tenir instal·lada la versió 1.4.2 o superior de la màquina virtual del Java. (Feu clic per començar ara la instal·lació)

Per fer la construcció, deixeu invisibles la graella i la finestra algebraica.

Dibuixeu cinc punts lliscants, de la manera habitual, i feu que no agafin, inicialment, cap valor igual a 0. A fi i efecte que quan interessi els poguem donar fàcilment un valor igual a 0 (per exemple si en l'experimentació volem fer que els alumnes treballin amb funcions de quart grau, o de tercer,… ) feu que l'increment en cada un d'aquests punts lliscants sigui 1.
Entreu l'expressió f(x)=a x^4+ b x^3 + c x^2 + d x+ e, que correspon a la funció que estudiarem.
Moveu els punts lliscants i comproveu les diferents formes que agafa la funció. Feu que es mostri com es veu a la figura, amb un color similar.
Entreu la comanda Extrem[f] i quedaran dibuixats els màxims i els mínims de la funció.²⁾
Entreu la comanda f'(x) i veureu la gràfica de la funció derivada que, com ja s'ha comentat, s'anomenarà g(x). Doneu-li un color diferent del de la funció f(x).
Entreu la comanda Arrel[g] i veureu com es dibuixen directament els punts de tall de la funció g(x) (que és f'(x)) amb l'eix d'abscisses.
Si dibuixeu uns segments verticals que uneixin cada extrem de la funció f(x) amb les arrels de la funció f'(x) quedarà més visible la relació que hi ha entre ells.

També es podria representar la segona derivada entrant, simplement, f ''(x). El que passa és que el gràfic potser quedaria poc clar i gens il·lustratiu.

Per això, el que fareu serà relacionar els punts d'inflexió de la funció f(x) amb els extrems de la funció f'(x).

Entreu la comanda PuntInflexió[f] i observeu que s'hi representen tots els punts d'inflexió de la funció f(x).
Entreu la comanda Extrem[g] i veureu els extrems de la derivada.
Dibuixeu, com abans, els segments verticals que permeten relacionar aquests punts (extrems de la derivada i punts d'inflexió de la funció).

Per entrar els rètols de la funció i la derivada:

Trieu l'eina Insereix un text i feu clic allà on voleu que es vegi.
Entreu el text
```
 "f(x) = "+f 
```
. Acabeu amb Aplica.
Repetiu el procediment per a la derivada, entrant el text ³⁾
```
 "f'(x) = " + g 
```

Acabeu els detalls estètics tal com us interessi… i guardeu la feina!

¹⁾ Si algú pregunta si es podria fer amb qualsevol altre tipus de funció, la resposta més aproximada és No, perquè la comanda Extrem que emprarem només actua eficaçment amb els polinomis i amb algunes altres -poques- funcions.

²⁾ Noteu que la comanda s'ha d'escriure en singular, Extrem[], i que es dibuixen alhora màxims i mínims. Convé indicar, també, que es mostren únicament els extrems i no tots els punts singulars. Si hi ha un punt amb derivada 0, és a dir amb tangent horitzontal, que no és un punt extrem -serà un punt d'inflexió-, aleshores aquest punt no apareix com a resultat de l'aplicació d'aquesta comanda.

³⁾ Veureu que, com sempre que es fan servir punts lliscants, el GeoGebra manté una escriptura formal "no operada" en la derivada. Però si feu una pràctica anàloga a aquesta entrant "a mà", cada vegada, la funció que us interessi aleshores la derivada apareixerà "ben escrita".