Introducció de la derivada d'una funció en un punt

En aquesta pràctica elaborareu una activitat que permet fer visual el concepte de derivada d'una funció en un punt.

• Es fa el càlcul de la taxa mitjana de variació ¹⁾ i es fa el pas a la taxa instantània de variació: derivada en un punt.
• Alhora s'acompanya aquest treball amb el que habitualment s'indica com la introducció geomètrica de la derivada. Veurem com es pot arribar al concepte de derivada en un punt observant com una successió de secants a la gràfica d'una funció tendeixen a una tangent, el pendent de la qual és precisament la derivada en el punt de tangència.

Podeu practicar movent el punt x = … que veieu sobre l'eix de les x i acostant-lo al punt a = … amb el benentès que podeu mostrar/amagar informació amb les caselles de verificació. També podeu variar la posició del punt a=… si voleu estudiar la derivada en un altre punt.

• Entreu a la casella d'entrada la funció f(x) = -x² / 5 + 3 x - 1. De fet podríeu entrar a qualsevol altra. Hem triat aquesta per tal que es vegi bé el que volem representar.
• Amb l'eina Punt nou dibuixeu un punt sobre l'eix d'abscisses, ben a la dreta de la pantalla.
• Canvieu el nom d'aquest punt per X2. Aquest serà el punt mòbil que acostarem al punt on volem estudiar la variació instantània de la funció.
• Escriviu a la casella d'entrada b = x(X2) i després A = (b,f(b)). Amb això heu representat el punt A sobre la gràfica de la funció que té com a primera coordenada la primera coordenada de X2.
• Entreu ara el punt B = (0,y(A)). Si desplaceu el punt X2 comprovareu que aquest punt B dóna el valor de la imatge del punt d'abscissa X2.
• Dibuixeu un altre punt sobre l'eix d'abscisses, per exemple el de coordenades (2, 0). Canvieu-li el nom per X1.
• Escriviu ara a la casella d'entrada a = x(X1) i, tot seguit, entreu el punt C = (a,f(a)) que veureu de seguida representat.
• Dibuixeu la recta que passa per A i C.
• Entreu el punt D = (0,y(C)).
• Dibuixeu els segments A B, X2 A, C D i X1 C.
• Feu que aquests segments es vegin amb una línia discontínua.
• Amb l'eina Insereix text entreu el text

  "f(a) = "+(f(x(X1)))

• Desplaceu-lo en el tauler gràfic de manera que es vegi bé, a prop del punt D.
• Repetiu el mateix procediment per al punt B, introduint el text

  "f(x) = "+(f(x(X2)))

• Dibuixeu una recta horitzontal (paral·lela a l'eix d'abscisses) que passi pel punt C.
• Trobeu la intersecció d'aquesta recta amb el segment X2 A. Serà el punt E.
• Dibuixeu els segments CE i AE. Feu que es vegin de color vermell.

La construcció està prou avançada. Si desplaceu el punt X2, veureu que la secant es va desplaçant. Ara bé, si el desplaçament de X2 fa que aquest punt quedi a l'esquerra de X1, alguna cosa falla… Anem a solucionar aquest petit problema.

• Desplaceu el punt X2 de manera que quedi a l'esquerra del X1.
• Dibuixeu una recta horitzontal que passi pel punt A.
• Trobeu la intersecció d'aquesta recta amb el segment X1 C. És el punt F.
• Dibuixeu els segments AF i CF i feu que es vegin de color vermell.

Tot seguit dibuixareu la tangent a la gràfica en el punt C.

• Desplaceu el punt X2 un altre cop de manera que quedi com estava inicialment.
• Trieu l'eina Tangents ²⁾ i feu clic sobre la gràfica de la funció i després sobre el punt C. Queda representada la tangent a la gràfica en el punt C.

Ara introduireu els textos que identifiquen la secant i la tangent.

• Obriu la finestra algebraica i comproveu quins noms ha posat el programa a les rectes secant i tangent.
• Canvieu aquests noms. Feu que siguin t el nom de la recta tangent i s el de la secant. Tanqueu la finestra algebraica.
• Amb el botó dret del ratolí obriu el pop-up que permet establir propietats dels objectes i seleccioneu aquestes dues rectes. Veureu que a la pestanya Àlgebra és possible escollir diferents maneres d'expressar-ne l'equació. Trieu l'opció Equació y = a x + b, que segurament serà la que estarà establerta per defecte.
• Introduïu-hi el text

  "Recta secant " + s 

  per identificar la secant i

  "Recta tangent " + t 

  per a la tangent.

• Situeu aquests rètols com us sembli més adient.

Acabeu ara els últims detalls de la construcció.

• Entreu el text

   "a = "+ a 

  associat al punt X1.

• Entreu el text

   "x = "+ b 

  associat al punt X2.

• Desplaceu-los per tal que es vegin bé i feu invisibles les etiquetes dels punts X1 i X2.
• Seleccioneu el segment AE i, amb el botó dret, accediu a Propietats. Feu que es vegi l'etiqueta, però només amb l'opció Valor activada. Feu el mateix amb el segment CE.
• Situeu un altre cop el punt X2 a l'esquerra del X1. Hi apareixen els segments AF i CF.
• Dibuixeu els punts mitjans d'aquests segments (amb l'eina corresponent, que trobareu al mateix grup que la de punt nou). Això ho feu per poder associar uns textos que faran d'etiquetes per tal que agafin valors negatius, com veureu tot seguit. Seran els punts G i H, respectivament.
• Trieu l'eina Insereix text, entreu el text

  b - a +""

  i, a la finestra de propietats, pestanya Posició indiqueu el punt G.

• Feu el mateix amb el text

   f(b) - f(a) + "" 

  i associeu-lo al punt H. D'aquesta manera, aquests valors són negatius. Feu que es vegin del mateix color que els segments.

• Feu invisibles tots els punts i les rectes que hem fet servir per a la construcció.
• Desplaceu el punt X2 i observeu el que passa.
• També podeu desplaçar el punt X1 i estudiar així la variació instantània en un altre punt.

Ara entrareu els textos finals.

• Entrareu unes noves variables per simplificar les expressions. Entreu n1 = f(b) - f(a).
• Entreu n2 = b - a. Aquí n2 representa el resultat del que en el gràfic apareix com x - a, que dóna la idea que x és l'abscissa mòbil.
• Trieu l'eina Insereix un text i feu clic en un lloc del tauler gràfic on voleu que hi vagi el primer text.
• Activeu l'opció Fórmula LaTeX; amb l'ajuda de la fracció que surt en el desplegable entreu ³⁾

   "TMV\;=\;\frac{f(x)-f(a)}{x-a}\;=\;\frac{"+n1+"}{"+n2+"}\;=\;"+(n1 /n2) 

Això és el que necessiteu entrar per tal que us surti una expressió semblant a

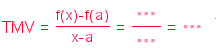
que representa la Taxa Mitjana de Variació entre x i a.

• Repetiu el procediment anterior amb el text

   "f'(a)\;=\;\lim_{x \rightarrow a}\frac{f(x)-f(a)}{x-a}\;=\;"+(Pendent[t]) 

  L'expressió que haurà sortit serà similar a:

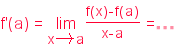
• Creeu una casella de verificació a la qual podeu posar de títol TMV i recta secant i hi podeu incloure el dibuix de la recta secant, el text corresponent a l'equació d'aquesta recta i el text que indica el valor de la TMV. Situeu-la on us vagi bé del gràfic.
• Actueu anàlogament amb una altra casella de verificació Recta secant i derivada per x=a. ⁴⁾

Ara només queda que modifiqueu els colors dels objectes i textos i la mida de les lletres per arribar a una construcció com la que podeu veure al principi de la pràctica.

Desplaceu els punts X2 i X1 i observeu els efectes, mireu que tot funcioni adequadament… i guardeu la feina!!!

Imagineu aquesta activitat en el marc d'una classe, amb una pissarra digital (encara que no sigui interactiva) i també en una aula d'informàtica amb treball individual per part de l'alumnat, amb unes instruccions de treball ben clares. Ben segur que penseu que disposar del GeoGebra és realment un valor afegit a la possibilitat d'escriure amb guix (ni que sigui amb guixos de colors) per a la lliçó d'introducció del concepte de derivada en un punt.