Teorema de Tales

En aquesta practica podreu visualitzar el teorema de Tales. Encara que no sigui estrictament un teorema de triangles, hi està molt relacionat. Per això, en la pràctica següent, veureu una aplicació a la semblança de triangles.

Una altra de les novetats que veureu és l'edició de text sobre la zona gràfica.

La figura que construireu serà com aquesta:

Moveu el punt lliscant i observeu com es conserva la proporcionalitat entre els quocients de determinades longituds, que podeu fer visibles o no gràcies a les caselles de verificació. També podeu moure els punts A, B i C. Comenceu la construcció.

• Definiu el punt lliscant a com ja ho heu fet en pràctiques anteriors, agafant 0 com a valor mínim i 14 com a valor màxim.
• Trieu l'eina Recta que passa per dos punts i feu clic dos cops per dibuixar la primera recta.
• Trieu l'eina Circumferència donats el centre i el radi i feu clic a sobre del punt A. Entreu com a radi a, que és el nom del punt lliscant.
• Trieu l'eina Recta que passa per dos punts i feu clic a sobre del punt A. Tot seguit, cliqueu per obtenir el punt C i dibuixar la segona recta.
• Trieu l'eina Intersecció de dos objectes i apropeu el cursor fins a la intersecció de la segona recta amb la circumferència. Quan estiguin seleccionades totes dues, feu clic. Quedarà dibuixat el punt D.
• Seleccioneu amb el botó dret del ratolí la circumferència i desactiveu l'opció Mostra objecte per fer-la invisible.
• Trieu l'eina Recta que passa per dos punts i feu clic a sobre del punt C i després sobre B. Quedarà dibuixada la primera secant a les dues rectes.
• Trieu l'eina Recta paral·lela i feu clic a sobre del punt D i, després, sobre aquesta última recta. Es dibuixarà una paral·lela a la recta anterior.
• Trieu l'eina Intersecció de dos objectes i apropeu el cursor fins a la intersecció d'aquesta recta i la recta que passa per A i B. Quan estiguin seleccionades totes dues, feu clic. Quedarà dibuixat el punt E.

Si ara moveu el punt lliscant, veureu com es desplaça la paral·lela. A continuació, definireu els segments que intervenen en la comprovació del teorema.

• Trieu l'eina Segment entre dos punts i cliqueu sobre el punt A i després sobre el D. Queda dibuixat el segment que anomeneu g.
• Feu el mateix amb tots els altres segments que es veuen en la finestra anterior, seguint l'ordre alfabètic indicat fins a dibuixar els segments h, i, j, k i l.

És convenient, abans de passar a escriure els rètols, que doneu color al dibuix:

• Accediu al menú Edita | Propietats, seleccioneu aquells segments que han de tenir el mateix color i trieu-ne el color corresponent.
• Feu el mateix amb les rectes.
• Seleccioneu tots els segments i trieu del desplegable de l'etiqueta l'opció Nom & Valor. D'aquesta manera, per a cada segment es veurà el nom i la seva longitud.

Ara és el moment de posar els rètols que es veuen en la finestra incrustada. El primer que posareu serà el del títol:

• Trieu l'eina Insereix text i feu clic sobre la part superior de la zona gràfica.
• S'ha obert una finestra. Aquí heu d'entrar el rètol: Teorema de Tales. Premeu Dàcord.

Com podeu observar, no es veu igual que en la figura inicial. Cal editar-lo:

• Seleccioneu el text amb el botó dret del ratolí i trieu l'opció Propietats.
• Feu servir els botons i desplegables que teniu a la vista per tal que sigui de color vermell, amb font de mida 18 i negreta (amb el botó que porta la lletra B). Acabeu amb Tanca.
• Amb l'eina Mou seleccionada podeu desplaçar el text.

A continuació, situareu els altres rètols. Fixeu-vos que alguns d'aquests tenen parts variables.

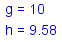
• Trieu un altre cop l'eina Insereix text i feu clic sobre la zona gràfica.
• Entreu el text exactament com es veu en la figura següent:

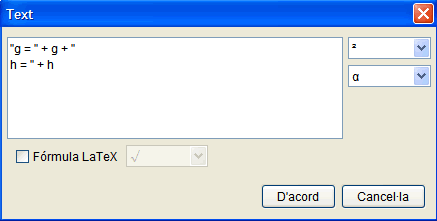
Aquest text té una part fixa i una altra variable. Analitzeu la primera línia. El text que hi ha entre cometes és la part fixa (g = ). No oblideu els espais en blanc. A continuació, escriviu un signe + per enganxar l'altra part, que és variable. Si escriviu després la lletra g sense cometes, voleu que aparegui al text el valor de g. D'aquesta manera, en moure el punt lliscant, el valor de g variarà i aquesta variació es reflectirà en el text.

Tot seguit, torneu a escriure +" i premeu la tecla Retorn per ubicar la resta del text a sota.

A continuació, repetiu el procés anterior per a la variable h.

Tots els rètols situats a sota del que acabeu de fer, la columna de rètols de l'esquerra, s'obtenen per aquest mateix procediment. Per obtenir sumes com g+i = 14.54, cal introduir "g+i= "+(g+i).

Els propers textos que entrareu, tota la columna de la dreta, són una mica diferents:

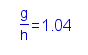
Fixeu-vos que la fracció està escrita de tal manera que no la podem reproduir fent servir només els del teclat.

• Trieu l'eina Insereix text i feu clic sobre la zona gràfica.
• Observeu el text que haureu d'escriure. Ara el comentarem.

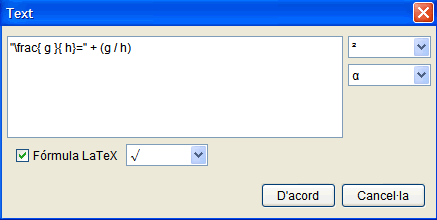
Els caràcters que hi ha entre cometes estan escrits en un llenguatge anomenat LaTeX, que permet escriure millor els símbols matemàtics.

• Activeu l'opció Fórmula LaTeX.
• Del desplegable, trieu l'opció de fracció.
• Poseu unes cometes davant i darrere de l'expressió que ha sortit en la finestra.
• Escriviu una g i una h al lloc que s'indica en la figura.
• Completeu la resta de l'expressió. Acabeu amb D'acord.

Ja teniu escrits els dos rètols variables, però amb una mida i un color diferent del de la mostra.

• Accediu a Edita | Propietats. Seleccioneu els dos textos que heu entrat i trieu les característiques de color i de mida que considereu oportunes. Acabeu amb Tanca.

Si ara seleccioneu l'eina Mou i moveu el punt lliscant observareu com els rètols variables s'actualitzen automàticament.

Repetiu tot el procés amb els altres rètols. Heu de tenir en compte que per als últims haureu de seguir els models:

• "g+i="+(g+i) 

• "\frac{g}{g+i}="+(g/(g+i))

Fixeu-vos que és totalment imprescindible fer servir parèntesis per indicar una operació entre variables.

Una vegada entrats tots els rètols podeu moure el punt lliscant i comprovar quines proporcions es compleixen i quines no. Esteu comprovant el teorema de Tales.

Per acabar, creeu les Caselles de verificació per mostrar/amagar els objectes que es veuen en la finestra, seleccionant correctament els textos que controlaran cadascuna.