Punts notables d'un triangle

Una de les possibilitats del GeoGebra és la de poder dibuixar una figura geomètrica, moure algunes de les seves parts i comprovar que determinades propietats es conserven. D'aquesta manera, es poden comprovar aquestes propietats i fins i tot induir-ne d'altres a partir de l'observació atenta d'aquests moviments. En aquesta pràctica comprovareu alguna d'aquestes afirmacions estudiant els punts notables d'un triangle.

En aquesta finestra teniu el resultat de l'activitat. Podeu moure els vèrtexs del triangle i observar-ne els resultats. També podeu activar o desactivar, tot fent clic a sobre, les opcions Mediatrius i Circumferència

Per al desenvolupament d'aquesta activitat és convenient prescindir dels eixos, de la graella i fins i tot de la finestra algebraica. Suposem que teniu activada l'opció Opcions | Etiquetes | Només els punts nous. De tota manera, recordeu que sempre que vulgueu que una etiqueta sigui invisible, ho podeu aconseguir seleccionant-la, o l'objecte que representa, amb el botó dret del ratolí i desactivar l'opció Mostra etiqueta. Per fer-la visible, naturalment, caldrà activar aquesta opció. En resum:

• Amb el botó dret del ratolí desactiveu les opcions Eixos i Graella.
• Accediu a Visualitza i desactiveu l'opció Finestra algebraica.

En primer lloc, dibuixareu un triangle qualsevol.

• Trieu l'eina Polígon i aneu clicant sobre la zona gràfica. Per cada clic es dibuixarà un vèrtex. Acabeu la figura clicant sobre el primer vèrtex que heu dibuixat.

A continuació dibuixareu el circumcentre del triangle.

• Trieu l'eina Mediatriu.
• Cliqueu, consecutivament, sobre dos vèrtexs del triangle o bé simplement sobre un costat i es dibuixarà la mediatriu corresponent.
• Feu el mateix amb els altres vèrtexs o costats.

Si ara obriu la finestra algebraica (accediu a Visualitza | Finestra algebraica) veureu que han sortit les equacions de les rectes dibuixades, que s'actualitzaran automàticament si moveu la figura.

• Trieu l'eina Intersecció de dos objectes i cliqueu, consecutivament, sobre dues mediatrius. Apareixerà el circumcentre dibuixat amb les seves coordenades a la finestra algebraica.
• Trieu l'eina Mou i moveu els vèrtexs del triangle. Observeu que tot s'actualitza. Torneu a tancar la finestra algebraica.

Tot seguit dibuixareu la circumferència circumscrita:

• Trieu l'eina Circumferència donats el centre i un punt per on passa, cliqueu sobre el circumcentre i, a continuació, sobre un vèrtex del triangle. Ja teniu la circumferència dibuixada.

Podeu obrir un altre cop la finestra algebraica i observeu que haurà sortit l'equació de la circumferència. Si moveu els vèrtexs, la figura segueix mantenint les seves propietats i la finestra algebraica s'actualitza constantment. Fixeu-vos que hi surten, i també s'actualitzen, les longituds dels segments i de la circumferència, i també de l'àrea (poly1) del triangle.

Podeu canviar, ara, els detalls estètics de la figura. Recordeu que per fer-ho el més pràctic és accedir a Edita | Propietats. Des d'aquesta finestra podeu fer tots els canvis. Si voleu que determinats objectes, com ara les mediatrius, tinguin el mateix aspecte, les podeu seleccionar, fent servir la tecla Ctrl i aplicar conjuntament les propietats. Feu diferents proves i acabeu prement Tanca. Deseu el fitxer.

Procedireu, ara, a crear les caselles que es veuen a la part superior dreta de la figura. Es tracta d'aconseguir que siguin visibles o invisibles, de manera voluntària, determinats elements de la construcció, simplificant el mètode emprat en el mòdul anterior((noteu que aquests procediments són ben diferents del d'esborrar els objectes. Si els esborréssiu, tots els objectes que en depenen també s'esborrarien!). Començareu per la casella per fer visibles o invisibles les tres mediatrius.

• Trieu l'eina Casella de verificació per mostrar/amagar els objectes i feu clic a la part superior de la zona gràfica.
• Escriviu Mediatrius a la casella Títol de la finestra que s'hagi obert.
• Amb l'eina Mou triada, moveu, si és necessari, la finestra que ha sortit per deixar visibles els objectes que hem de triar.
• Feu clic sobre una de les mediatrius. Observeu com el seu nom apareix a la llista de la finestra de la casella de verificació.
• Feu clic sobre les altres mediatrius i s'aniran incorporant a la llista. També les podríeu haver triat del desplegable.

La finestra haurà quedat així:

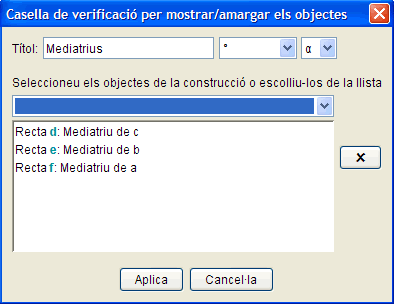
• Acabeu amb Aplica.

La casella de verificació s'haurà creat. Amb l'eina Mou triada, la podeu desplaçar. Amb aquesta mateixa eina activada, feu clic a sobre diverses vegades i observeu el que passa.

Si accediu a la finestra algebraica, veureu que en l'apartat d'Objectes lliures s'haurà creat una nova variable, segurament anomenada h, que agafa els valors true o false segons si tenim validada o no la casella de verificació que heu creat. Aquest tipus de variable s'anomena Variable boleana o Valor boleà.

• Accediu al menú Edita | Propietats i seleccioneu de l'esquerra les mediatrius que estat en l'apartat de rectes.
• Amb aquesta selecció feta cliqueu la pestanya Avançats i veureu que a la casella Condició per mostrar l'objecte surt la mateixa lletra que donava nom a la Variable boleana creada.

Quan un objecte té en aquest apartat el nom d'una variable boleana significa que està controlat per la casella de verificació corresponent. Si l'esborréssim es lliuraria d'aquest control. Aquest és un bon mètode per incloure i excloure objectes del control d'una casella de verificació.

• Repetiu el procés anterior per crear la Casella de verificació per mostrar/amagar els objectes que controli la visibilitat de la circumferència. Cal que trieu del desplegable la circumferència (l'anomena cercle) o bé la trieu directament de la zona gràfica. El títol de la casella pot ser Circumferència.
• Comproveu el nom de la variable boleana corresponent a aquest casella.
• Aneu a les propietats de la circumferència per observar que aquest nom és a la casella Condició per mostrar l'objecte de l'apartat Avançats.

En aquest moment podeu anar movent els vèrtexs, amb l'eina Mou seleccionada, i comprovar-ne algunes propietats:

• Quan queda el circumcentre a l'exterior del triangle?
• Quan queda a l'interior?
• Quan queda sobre un costat? Sobre quin?

Per continuar la construcció dels altres punts no esborreu la figura anterior perquè, d'aquesta manera, anireu fent servir el mateix triangle per als altres punts. Això sí, podeu mantenir invisibles les mediatrius i la circumferència.

També canviareu el nom del punt:

• Amb el botó dret del ratolí, seleccioneu el punt D.
• Accediu a l'opció Canvia de nom, escriviu com a nom nou Circumcentre i acabeu prement D'acord.

Per començar, haureu de dibuixar els punts mitjans dels costats.

• Trieu l'eina Punt mitjà o centre.
• Cliqueu sobre cadascun dels costats. Apareixeran els tres punts mitjans.

Només queda dibuixar les mitjanes.

• Trieu l'eina Recta que passa per dos punts i cliqueu sobre un vèrtex i, a continuació, sobre el punt mitjà del costat oposat. Repetiu aquest procediment per als tres vèrtexs.

El Baricentre quedarà determinat:

• Trieu l'eina Intersecció de dos objectes i cliqueu, consecutivament, sobre dues de les mitjanes.

Com ja heu fet en l'apartat anterior, podeu canviar el color del punt, el seu nom (poseu-li Baricentre) i fer invisibles els punts mitjans dels costats. Per a les mitjanes, creeu una casella de verificació com en l'apartat anterior.

• Moveu els vèrtexs i comproveu-ne algunes propietats.

A partir de la figura anterior, ara dibuixareu l'ortocentre. Per començar, heu de dibuixar les alçades. En realitat, n'hi haurà prou de dibuixar rectes perpendiculars a cada costat que passin per cada vèrtex oposat.

• Trieu l'eina Recta perpendicular i cliqueu sobre un vèrtex i, tot seguit, sobre el costat oposat. Repetiu aquest procediment amb els altres costats.
• Trieu l'eina Intersecció de dos objectes i cliqueu, consecutivament, sobre dues de les rectes.
• Repetiu el procediment de l'apartat anterior per acabar els detalls estètics.
• Creeu una casella de verificació per a les altures, com ja heu fet en els apartats anteriors.

Una de les propietats que es desprenen de l'observació d'aquests punts quan movem els vèrtex del triangle és que sempre estan alineats. Determinen l'anomenada Recta d'Euler.

• Trieu l'eina Recta que passi per dos punts i feu clic, consecutivament, sobre el baricentre i el circumcentre. Ja teniu la recta d'Euler dibuixada.
• Creeu una casella de verificació per a aquesta recta.

A continuació, podeu comprovar que, efectivament, la recta passa també per l'ortocentre:

• Trieu l'eina Relació entre dos objectes.
• Feu clic, consecutivament, sobre la recta i l'ortocentre i observeu el missatge que surt.

D'aquesta manera es pot assegurar que la recta d'Euler passa pels tres punts. Moveu els vèrtexs del triangle.

Si ara obriu la finestra algebraica podeu observar totes les equacions i les coordenades dels diferents objectes que han anant sortint.

Ara encara falta dibuixar l'incentre. Aquest punt, intersecció de les tres bisectrius, té, entre d'altres, la propietat de ser el centre de la circumferència inscrita. El dibuix del punt i de la circumferència serà uns dels exercicis d'aquest mòdul.

Després d'haver fet totes aquestes pràctiques, fareu un cop d'ull a la finestra algebraica.

• Accediu al menú Visualitza i activeu l'opció Objectes auxiliars, si no ho està.
• Del mateix menú activeu Finestra algebraica (o premeu Ctrl+A). Apareix la finestra algebraica:

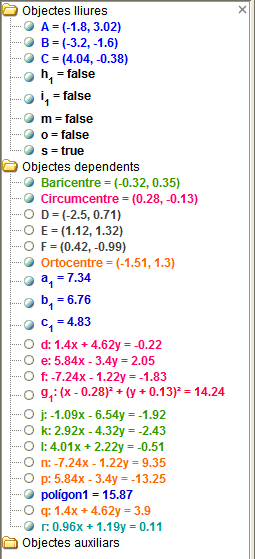
Noteu que a l'apartat Objectes lliures teniu els tres punts inicials del triangle i les caselles de verificació. Tota la resta d'objectes han anat a parar a Objectes dependents. Podeu passar alguns d'aquests objectes a Objectes auxiliars. Fixeu-vos també que aquells que tenen la petita circumferència de color blanc són els que, en aquest moment, són invisibles. Si feu clic a sobre d'aquestes petites circumferències podeu canviar la propietat de visibilitat.

• Seleccioneu, fent servir la tecla Ctrl, tots els objectes tret del tres punts notables i la recta d'Euler.
• Amb els objectes seleccionats premeu el botó dret del ratolí i activeu l'opció Objecte auxiliar i finalment Tanca.

Ara tots aquests objectes han passat a l'apartat Objectes auxiliars. Si voleu, podeu amagar aquests objectes accedint a Visualitza i desactivant l'opció Objectes auxiliars.