Com ja us hem presentat, una novetat important del GeoGebra 4 és la incorporació dinàmica del càlcul algebraic simbòlic (CAS) en una nova finestra. Això augmenta moltíssim el potencial del GeoGebra.

Aquells que ja useu el Maxima o coneixeu altres calculadors simbòlics clàssics com ara Derive, Mathematica o Wiris hi veureu algunes similituds. Això sí, ara en programari lliure i sense necessitat d'haver d'instal·lar res més.

Per qui en vulgui saber una miqueta més us fem saber que el nou GeoGebra no utilitza cap nou CAS, sinó que mira d'integrar altres eines de programari lliure ja funcionen de manera contrastada i aprofitar-ne la feina feta.

Quan entrem un comandament de CAS en una versió WebStart del GeoGebra s'executa un motor de càlcul algebraic anomenat MathPiper, en canvi, en treballar en local, el GeoGebra revisa si en aquesta màquina hi ha instal·lat el Maxima per aprofitar-ne tota la seva potència.

La següent imatge mostra que en demanar al GeoGebra que calculi la derivada de l'expressió ax³ respecte la variable x la resposta és 3 ax² independentment de quin hagi estat el motor de càlcul CAS que internament s'hagi usat.

Tot seguit podreu practicar algunes coses amb el CAS incorporat al GeoGebra, però us volem fer una important reflexió sobre l'exemple que s'acaba de mostrar.

En general els calculadors algebraics simbòlics creen la necessitat que els usuaris coneguin molts comandaments.

Com ja sabeu l'equip del GeoGebra treballa per posar-nos les coses el màxim de fàcils.

La incorporació del CAS es pot fer en una nova finestra flotant del GeoGebra . En ella podreu entrar els comandamanents per escrit o mitjançant botons.

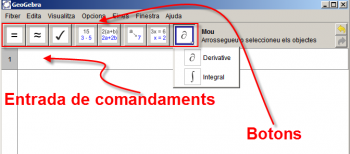
Cal destacar que no només es tracta d'incorporar el càlcul simbòlic, sinó que és important remarcar que, com veureu, a més a més hi ha un lligam dinàmic amb la resta d'objectes.
Tot seguit podreu fer algunes proves amb uns exemples molt breus. Experimenteu vosaltres mateixos i segur que us sorprendreu.

En el següent vídeo podreu observar com es poden calcular derivades de diferents maneres.

• Es pot calcular, com hem dit, la derivada de l'expressió
• 3ax² on a no cal ni haver-la definit, per tant GeoGebra interpreta a com un paràmetre
• En canvi, podeu definir un punt lliscant b i calcular la derivada de l'expressió bx³ i provar de fer variar el paràmetre b i veure'n la repercussió dinàmica

Comproveu-ho amb el següent vídeo

Les matrius s'han d'escriure com una llista de llistes. Per exemple heu d'entrar {{1,0},{0,1}} per treballar amb la matriu Identitat.

En la següent imatge podreu veure un exemple amb matrius, el quadrat d'una matriu, la seva inversa o el seu determinant. Proveu de repetir els passos:

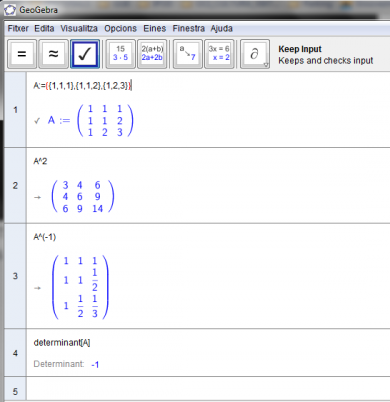
• Al menú Visualitza seleccioneu només treballar amb la finestra CAS
• La drecera de teclat Ctrol + Shift + D activa o desactiva la finestra CAS. Ara podeu ocultar les altres finestres
• Definiu la matriu A (observeu que podeu fer la definició usant A := )
• Situats a la segona línia, feu clic la matriu de la primera línia marcada en color blau, amb això la matriu s'haurà copiat a la segona línia i només haureu d'indicar que en voleu fer el quadrat. Podeu escriure ^2
• De la mateixa manera, situats a la tercera línia, seleccioneu novament la matriu A de la primera línia i escriviu ^(-1). Comproveu si en fa la matriu inversa? I si escriviu Inversa[A]? Proveu el comandament Inverteix[A]
• Tot plegat, com haureu pogut comprovar, cal tenir les coses ben clares en usar el CAS… Proveu el comandament Transposa[A]
• Després calculeu-ne el Determinant. Podeu escriure Determinant[] parant atenció amb el text predictiu i seleccionant la matriu A
• En acabat proveu de fer algun canvi a la primera línia, la de definició. Veureu com tots els càlculs s'actualitzen dinàmicament

En el següent vídeo podreu comprovar quins passos cal seguir per simplificar una fracció algebraica factoritzant-ne primer el numerador i després el denominador.