Funcions de segon grau. Paràboles

Tal com ja hem fet en la pràctica anterior, trobareu en els exercicis la proposta d'elaborar, amb un disseny propi, una activitat que mostri que una funció polinòmica de segon grau y = a·x² + b·x + c té com a gràfica una paràbola i quina és la influència dels coeficients a, b, c. Per realitzar l'exercici podreu adoptar l'enfocament i el punt de vista que més us convinguin.

Ara, "per entrar en matèria" i suggerir-vos algunes idees didàctiques, com a pràctica dirigida teniu una activitat que mostra com es pot raonar quina és la gràfica d'una paràbola mitjançant "la completació de quadrats". Així es visualitza la transformació de la gràfica de y=x² en la de y = a·(x+v)² + w i es justifica quin és el vèrtex de la paràbola.

• Desplaceu els punts lliscants que fan variar els paràmetres a, v, w i observeu què passa. L'objectiu és aconseguir que la paràbola blava coincideixi amb la vermella.
• Si voleu recomençar l'activitat amb una nova paràbola en estudi (la corba vermella) i amb la corba blava en la posició inicial només cal que cliqueu sobre la icona de la part superior dreta de la finestra, que té justament aquesta finalitat quan s'està treballant en una pàgina web. Ara bé, tant si treballem en línia com si ho fem amb el programa instal·lat al nostre ordinador, també tenim les opcions Ctrl+r o F9 que generen nous nombres aleatoris i, per tant, una nova paràbola vermella; si ho feu així, la paràbola blava inicial no serà la "estàndard" sinó la que teníeu en el moment de prémer Ctrl+r o F9.
• Si activeu la casella de verificació, veureu l'expressió de la paràbola vermella.

Per elaborar aquesta activitat en una finestra nova del GeoGebra, podeu procedir així:

• Definiu a la línia d'entrada la funció p(x)= x^2. Aquesta és la que podem anomenar "paràbola estàndard".
• Entreu la llista param = {-4, -3, -2, -1, -0.5, -0.25, 0.25, 0.5, 1, 2, 3, 4}. Aquesta llista conté els valors possibles del coeficient que multiplica la x² de la paràbola vermella.
• Definiu, de la manera habitual, tres punts lliscants i feu que els seus noms siguin a, v, w. Accediu a Propietats amb el botó dret del ratolí, per tal d'aconseguir que el punt lliscant a vagi de -4 a 4 amb un increment de 0.25. Els altres dos han d'anar de -4 a 4 amb un increment d' 1. Situeu-los al lloc adient de la zona gràfica.
• Definiu a la línia d'entrada el numèric aa=AleatoriEntre[1, 10]. Aquest comandament genera nombres aleatoris enters des de l'1 fins al 10.
• Definiu ara at=Element[param, aa]. D'aquesta manera, a partir del nombre aleatori generat per aa, s'obtindrà un element de la llista param com a valor per at.
• Definiu també vt=AleatoriEntre[-4, 4] i wt=AleatoriEntre[-4, 4], que són els nombres aleatoris per als altres paràmetres de la paràbola vermella.

A continuació, definireu les dues paràboles: la blava, que es controlarà a partir dels punts lliscants a, v i w, i la vermella, que es dibuixarà a partir dels valors aleatoris generats per at, vt i wt.

• Definiu q(x)=a*(x + v)^2+w (paràbola blava) i f(x)=at*(x + vt)^2+wt (paràbola vermella). Accedint a Propietats feu que tinguin els colors corresponents i que l'estil de q(x) sigui de línia discontínua.

• Desplaceu els punts lliscants i veureu com varia la gràfica de q(x). Premeu Ctrl+r o F9 i veureu com es generen el nombres aleatoris per als paràmetres at, vt i wt i, per tant, la gràfica de f(x) va variant.

• Finalment, amb l'eina Insereix text podeu incloure els dos textos que indiquen en cada moment quina és la funció en estudi (corba vermella) i l'expressió de la funció que mostra la paràbola que es va transformant (corba blava, de punts).

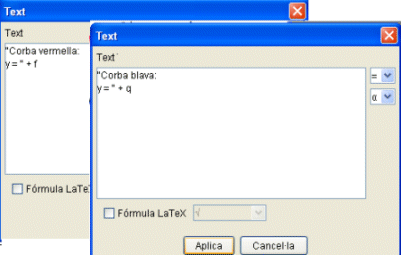
• Després de definir els dos textos anteriors situeu-los al lloc que cregueu convenient de la zona gràfica (clicant amb el botó esquerre els podeu situar a mà) i doneu-los els aspectes de presentació que us interessi. Ho heu de fer, com ja sabeu, amb el botó dret i Propietats; a l'exemple s'ha variat el color, s'ha fet que el text aparegui en negreta i s'ha augmentat la mida a 14 punts.

• Amb l'eina Casella de verificació per mostrar/amagar els objectes feu que sigui visible o invisible el text corresponent a la paràbola vermella.

I ja teniu l'activitat construïda. Guardeu la feina!