Punts de tall: equacions i sistemes amb el GeoGebra

En aquesta pràctica es treballen amb el GeoGebra els procediments que, de vegades, es coneixen amb la denominació d' Interpretació geomètrica de la resolució d'equacions i sistemes, es comenten alguns recursos de càlcul directe incorporats al programa i es fa una primera presentació de les còniques del pla.

Observeu la finestra activa següent del GeoGebra. Experimenteu-hi movent paral·lelament la funció i observeu què succeeix amb els punts de tall, és a dir, les arrels del polinomi.

Per fer un estudi anàleg a l'anterior només cal:

• Definir la funció f(x), que ja sabeu que es dibuixa automàticament.
• Aplicar un dels dos procediments següents per trobar els punts de tall:
  • L'eina Intersecció de dos objectes aplicada a la gràfica de la funció i l'eix d'abscisses.
  • El comandament Arrel[f] (o també Arrel[f(x)]).
  • Tant d'una manera com de l'altra els valors de les arrels són un conjunt. Intenteu esborrar una sola de les arrels i observeu què passa.

Canvieu la funció per a algunes altres funcions polinòmiques (que no cal que siguin de grau 4 i que, si voleu, podeu entrar com a productes indicats) i repetiu l'estudi; de seguida us adonareu que el GeoGebra té incorporats mètodes numèrics que donen directament totes les arrels d'una equació polinòmica, tant si es poden calcular exactament com si no. A l'apartat següent veureu les diferències amb el cas de funcions transcendents.

En la pràctica anterior se us ha proposat que adeqüéssiu els eixos per estudiar quants punts comuns tenen les gràfiques de les funcions f(x)=2006^x i g(x)=2007x+2008. Segurament ja heu trobat la solució, i també és ben probable que ja hagueu experimentat per què, a més de saber respondre la qüestió de quants punts comuns?, pugueu dir ràpidament quins són els punts comuns?

La imatge següent mostra la solució:

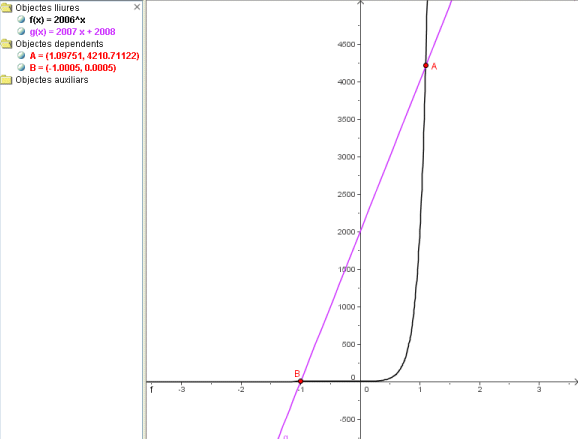
• S'hi han entrat les dues funcions.
• S'ha accedit a modificar les propietats de la zona gràfica posant a la pestanya de l'Eix X que el mínim sigui -4 i que el màxim sigui 4 (així es defineix l'interval de valors de x que es visualitza) i a la pestanya de Eix Y de -1000 a 5000. Fent això queda del tot clar que hi ha dos punts comuns.
• Ara bé, a diferència del que s'ha vist amb les funcions polinòmiques, succeeix que amb aquestes funcions l'eina Intersecció de dos objectes només dóna una sola solució ¹⁾, i aleshores caldrà fer diverses vegades el procediment, una a prop de cada punt d'intersecció, per trobar-los tots.
• Finalment, com que inicialment apareixia com un dels punts comuns (-1, 0) que, evidentment, no ho és de manera exacta, convé accedir al menú Opcions i fer que es mostrin 5 posicions decimals.

Així, direu, ja s'ha resolt l'equació 2006^x = 2007x + 2008 i també un sistema d'equacions. Efectivament!

Ara bé, per resoldre aquesta equació també es pot analitzar la funció F(x) = 2006^x - 2007x − 2008 i estudiar quins són els punts en què talla l'eix de les x. Aquest és el procediment que es reflecteix en la propera imatge:

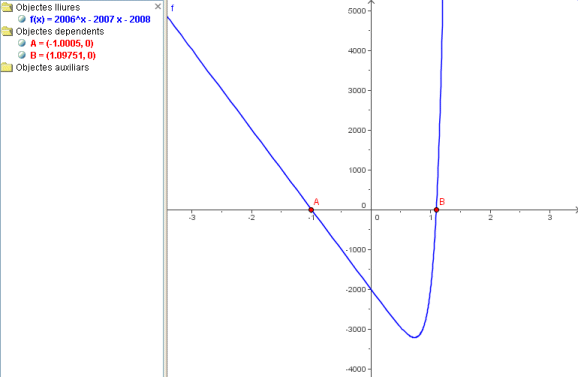
Com en el cas anterior es poden trobar els punts que busqueu amb dos procediments, però, com a característica conceptual dels mètodes numèrics, cada vegada obteniu una sola solució. Què cal fer si les volem trobar totes?

• Amb l'eina Intersecció de dos objectes trobareu, habitualment, l'arrel més propera als punts de la corba i de l'eix de les x on cliqueu. Si ho aneu fent successives vegades, anireu trobant les diverses arrels.
• Amb el comandament Arrel[F] (o també Arrel[F(x)]) trobareu una solució que depèn del valor que pren per defecte el programa per començar les iteracions. Si no dieu res en contra, serà sempre la mateixa solució, però podeu precisar…
  • Si apliquem el comandament Arrel amb dos arguments, Arrel[F, a], que són la funció i un nombre real, aleshores el programa aplica el mètode de Newton per trobar una solució de F(x)=0 començant les iteracions per x₀ = a.
  • Si apliqueu el comandament Arrel amb tres arguments, Arrel[F, a, b], que són la funció i dos nombres reals, a < b, aleshores el programa aplica el mètode de la bisecció (o de Bolzano) per trobar una solució de F(x)=0 situada a l'interval [a, b].
• Experimenteu amb la funció F(x) = 2006^x - 2007x - 2008 aplicant-hi…
  • Arrel[F,-2]
  • Arrel[F,1]
  • Arrel[F,-2, 0]
  • Arrel[F,0.5, 1.1]

A diferència dels exemples que hem vist amb les funcions polinòmiques, ara cadascuna de les solucions que hi ha és un objecte únic. Si moveu interactivament les funcions i alguna de les solucions desapareix, veureu l'habitual Objecte no definit; a la inversa, si apareixen noves solucions pel fet de variar les funcions, aquestes noves solucions no apareixeran si no feu una nova aplicació de l'eina Intersecció de dos objectes.

En l'apartat anterior heu vist la interpretació geomètrica de la recerca de les solucions d'un sistema d'equacions del tipus 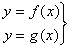amb la utilització d'eines de càlcul numèric, si escau, per trobar individualment les solucions.

En la situació anterior, si les dues funcions que apareixen són polinòmiques es troben totes les solucions. Imagineu el problema que té l'enunciat i voleu trobar-ne la solució amb el GeoGebra. La imatge següent en dóna exemple per a un valor concret de a:

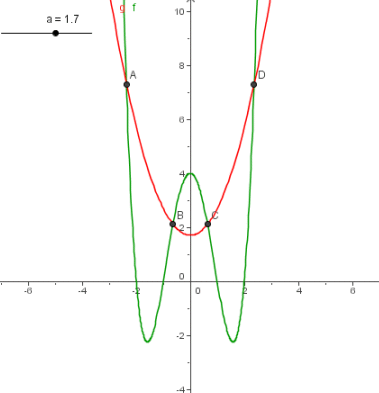
• Construïu un punt lliscant i poseu-li com a interval de variació de -8 a 8.
• Definiu les dues funcions f(x) i g(x).
• Aneu variant el valor del punt lliscant i trobareu la solució del problema plantejat.

Si canvieu les funcions que intervenen en l'enunciat el procediment serà exactament el mateix, però, de vegades, la precisió del càlcul no permetrà reconèixer exactament les situacions de tangència. ²⁾

És molt important comentar que amb el GeoGebra també podeu estudiar gràficament sistemes de dues equacions lineals o quadràtiques, és a dir les interseccions de rectes o còniques, a partir de la idea fonamental que es pot entrar l'equació implícita d'aquests objectes.

En un dels exercicis del mòdul se us proposa estudiar alguns d'aquests sistemes (concretament, que elaboreu una activitat per estudiar els sistemes d'equacions lineals) i a continuació estudiareu els sistemes que geomètricament representen la intersecció d'una recta i una cònica.

Tot seguit en teniu un exemple:

• Entreu a la finestra de comandes i escriviu 4x-3y=-5.
  Veureu que s'ha dibuixat la recta corresponent. Podeu donar-li el nom de r.
• Entreu ara a x²+2y²-8x-17y=-40. Veureu que es dibuixa una el·lipse.
• Comproveu que a la finestra algebraica s'identifiquen correctament les dues figures:
  

.

• I ara, amb l'habitual eina Intersecció de dos objectes, ja podeu observar de seguida quants i quins són els punts d'intersecció.
• Desplaceu la recta o l'el·lipse i observeu què succeeix.

Feu altres proves amb rectes i còniques que podeu entrar a la finestra algebraica redefinint la que us interessi; tanmateix, l'estudi de les còniques s'aprofundirà en el mòdul següent.

• Observeu les diverses còniques possibles i vegeu que el GeoGebra en fa una classificació acurada a partir de la seva expressió analítica.
• Exemples proposats:
  • 3x² + y² - 5x = 0
  • 3x² - y² - 5x = 3
  • 2x - y² +2y - 3 = 0
  • x² - 4y² = 0
  • y² - 9 = 0

Investigueu! I, si apareixen dubtes, no tingueu recança a preguntar!