Funcions i gràfiques

En aquesta pràctica constatareu que el GeoGebra, a més de Geometria i àlGebra també té molts recursos en el camp de l'anàlisi. Fareu una primera passada, que ja veureu que es pot dur a terme ben àgilment, per les funcions i l'estudi de les seves gràfiques. En el mòdul 6 reprendrem el tema amb les eines del càlcul infinitesimal.

La imatge següent correspon a una de les activitats que us suggerirem més avall, on introduirem l'ús de la traça d'un punt: s'explica què representa la gràfica d'una funció i es distingeix visualment, de manera interactiva, per cada valor de la variable independent, quin és el signe del valor que pren la variable dependent.

Engegueu el GeoGebra. Per treballar amb funcions serà imprescindible que els eixos siguin visibles, i en alguns casos també pot ser interessant que aparegui la graella; per veure millor les fórmules podeu accedir al menú Opcions i augmentar la mida de la lletra a 16 pt. Tot seguit veureu que per representar la gràfica d'una funció n'hi ha prou amb escriure'n l'expressió formal.

• Col·loqueu el cursor a la línia d'entrada de comandaments i funcions, escriviu-hi f(x)=x³/32 - 2x i cliqueu Retorn. Per posar l'exponent teniu dues opcions:
  • o bé fer servir la sintaxi del LaTeX, a saber x^3,
  • o bé emprar el desplegable que teniu a la part inferior de la pantalla. .
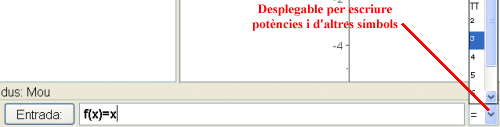• Veureu que s'ha dibuixat la gràfica de la funció anterior, però amb els eixos situats de la manera que el programa en diu Vista Estàndard. Per modificar aquesta vista:
  • Podeu fer servir l'eina Desplaça la zona gràfica i així moure els eixos "a mà", paral·lelament, sense canviar-ne la graduació.
  • Podeu fer clic amb el botó dret sobre la zona gràfica i triar Propietats. Veureu que hi ha dues pestanyes Eix X i Eix Y, que permeten personalitzar amb tot detall els eixos. Així podeu centrar l'origen de coordenades si això és el que us interessa. Si feu un canvi d'aquest tipus, però voleu tenir la seguretat que manteniu la mateixa unitat als dos eixos, acabeu posant EixX : Eix Y = 1:1, ja sigui en el mateix quadre de diàleg de Propietats, ja sigui en el menú que surt quan es clica amb el botó dret a la Zona Gràfica.
• Investigueu i feu proves amb altres funcions.
• Si voleu saber la llista completa de funcions incorporades al GeoGebra, aneu a l'Ajuda i, aleshores, a Search cerqueu Operacions. Trieu l'opció Funcions pre-definides i operacions.
• Comproveu que la gràfica d'una funció és un objecte global per al GeoGebra i que podeu moure'l paral·lelament. Adoneu-vos de la forma com el programa ens dóna la nova equació.

Com que ja us hem suggerit d'anar al quadre de Propietats de la zona gràfica, segurament ja heu investigat la manera més ràpida d'adequar la gràfica d'una funció per a una primera visualització, que comentem en la imatge següent.

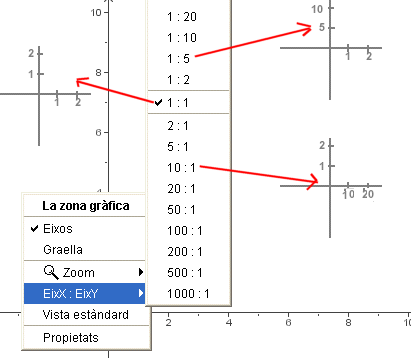
• Accediu al GeoGebra. Representeu la funció f(x) = (x-2)(x-8)(x+5).
  • Heu de saber que podíeu haver-la escrit, també, f(x) = (x-2)*(x-8)*(x+5). Tot i que el GeoGebra entén la juxtaposició com a producte, en algun moment pot ser més clar escriure el signe de producte, que és l'asterisc.
  • Ara penseu si serà millor activar l'opció Eix x:Eix y = 1:20 o bé Eix x:Eix y = 20:1 i comproveu que, amb l'elecció encertada, la gràfica ja es visualitza de manera adequada.
     
    
• Perquè investigueu una mica pel que fa a l'optimització de la graduació dels eixos, us proposem un exercici que resoldrem amb detall en la pràctica següent. Quants punts comuns tenen les gràfiques de les dues funcions f(x) = 2006^x i g(x) = 2007 x + 2008?¹⁾

En la finestra activa següent es genera, punt a punt, la gràfica d'una funció i es visualitzen de colors diferents els punts de la gràfica segons que el valor de la imatge sigui positiu o bé negatiu.

Moveu el punt original (el que dóna el valor de la variable independent) sobre l'eix de les x i observeu.

Per elaborar aquesta activitat, podeu procedir així:

• Definiu la funció. La que heu pogut veure és: f(x)=x³/32 - 2 x.

• Com que voldrem moure punts, per assegurar que la funció que estudiem romangui fixa i no es desplaci, cliqueu amb el botó dret sobre la definició de la funció a la finestra algebraica, o sobre la gràfica de la funció a la zona gràfica, i aleshores trieu Propietats i activeu Fixa objecte.

• Definiu un punt sobre l'eix de les x, que serà el punt que mostra el valor de la variable independent que ens interessa en cada moment (el que en el llenguatge funcional se'n diu, també, l'original). Manteniu el nom A per al punt; després ja el canviareu.
• Definiu a la línia d'entrades un punt B amb l'expressió B = (x(A), f(x(A))). Com ja sabeu, aquest és el punt que defineix la gràfica.
• Seleccioneu el punt B i, amb el botó dret del ratolí, accediu a Propietats.

• Aneu a la fitxa Avançat i entreu a la casella Vermell l'expressió y(B) >= 0 i, a continuació premeu Intro. Veureu que l'expressió s'ha convertit en y(B) ≥ 0 (aquesta és una manera d'escriure el símbol ≥), i que han aparegut zeros a les altres caselles.

Amb aquesta última acció heu introduït una condició. Això significa que si la segona coordenada del punt B és més gran o igual a zero, el valor del color vermell serà igual a 1 i, en cas contrari, valdrà 0.

• Entreu a la casella Blau l'expressió y(B)< 0 i premeu Intro.

En aquest cas, la condició ens diu que si la segona coordenada de B és negativa, el valor del color blau serà igual a 1 i, en cas contrari, serà igual a 0.

• Acabeu amb Tanca.

Desplaceu el punt A i veureu com el punt B va canviant de color segons el signe de la funció.

Aquesta activitat que tot seguit acabareu serveix com a presentació de l'opció que fa visual el traç d'un punt quan es mou interactivament un gràfic. Al diccionari de l'IEC trobem: Traç. Senyal que fa un llapis, una ploma, etc., sobre el paper en escriure o en dibuixar i nosaltres podem veure'n una aplicació virtual si imaginem que un punt que es mou per la pantalla de GeoGebra hi va deixant un senyal. Això farem per al punt B.

• Obriu la finestra de Propietats. Seleccioneu el punt B. Feu que no es mostri l'etiqueta i cliqueu a Activa el traç. A la pestanya Estil feu que la mida dels punts sigui 2.

Feu proves i vegeu que tot va per bon camí, tal com ho volíem. Tal vegada observeu que els punts que deixa el traç queden més separats que a la finestra interactiva amb què heu practicat. Si ho voleu tenir com a la finestra:

• Accediu a les propietats del punt A com ho feu habitualment. A la pestanya Àlgebra veureu que hi ha una casella on es pot establir Increment. Feu proves posant-hi 0.025 o 0.01. Recordeu, també, que el punt A el podeu moure amb el ratolí, o també seleccionant-lo, i aleshores moure'l amb les fletxes de cursor.
• Accediu també al menú Opcions | Enganxar els punts a la graella i trieu l'opció Inactiu.

Tot seguit dibuixareu els segments que ensenyen, per cada valor de la variable independent, quin és el valor de la variable dependent i enllestireu els darrers detalls per tenir l'activitat tal com s'ha presentat.

• Definiu a la finestra de comandes un punt E=(0, f(x(A))).
• Amb l'eina Segment entre dos punts definiu els segments AB i BE. Aneu a Propietats i trieu l'estil de recta adequat (línia de punts).
• Funció: feu que no es mostri l'objecte.
• Punt A: canvieu-li el nom i que sigui Original.
• Punt E: canvieu-li el nom i que sigui Imatge.
• Finalment, amb l'eina Insereix text, creeu un text que sigui Punt de la gràfica. Seguidament modifiqueu les propietats d'aquest text a la pestanya Posició perquè tingui com a Punt origen el punt B. Tant les etiquetes dels punts A i E com aquest text fixat al punt B es poden acabar de situar a mà.

 
Deseu la feina i experimenteu. Si voleu provar amb una altra funció, primer de tot haureu de desactivar a la finestra de propietats de la funció el Fixa objecte que heu establert per a la funció, i aleshores podreu canviar-la.

Segur que en les proves que heu fet per a la representació de funcions n'heu representat algunes que no tenen com a domini tot el conjunt. Haureu vist que es representen correctament, restringides al seu domini.

• Assageu amb f(x) = sqrt(x) o bé amb g(x) = log (x2 - 1). Proveu què succeeix si escriviu g(0.5) o bé g(1) o bé g(4).

En moltes aplicacions científiques interessa considerar funcions que només estan definides en un interval. Això ho podem aconseguir mitjançant el comandament Funció, que té com a arguments la funció i els dos extrems de l'interval on volem que estigui definida.

• Podeu provar-ho amb f(x) = Funció[4+sin(3x),0,π].
  • El nombre pi el podeu escriure així mateix (és a dir pi, que és una variable pròpia del sistema) o amb la lletra grega (π), cosa que es pot fer amb el mateix desplegable que hem comentat per als exponents o bé amb el desplegable de les lletres gregues; a diferència de les altres lletres gregues, la π no serveix per a definir variables en el GeoGebra.
  • Estudieu què succeeix si demaneu f(0) o bé f(2π) per a la funció anterior.

• Feu més proves.

En altres ocasions interessa considerar funcions definides a trossos. Això passa molt sovint als exàmens que es proposen als alumnes de Batxillerat. Vegeu-ne un exemple:

Tot seguit podeu experimentar amb el GeoGebra i els dos punts lliscants que representen els paràmetres que apareixen a l'enunciat per buscar la solució al problema plantejat. Us pot anar bé recordar que, quan teniu seleccionat un punt lliscant, les tecles de Fletxa amunt (o també Fletxa dreta) i Fletxa avall (o també Fletxa esquerra) serveixen per variar-ne el valor numèric, augmentant-lo o disminuint-lo respectivament en la quantitat assenyalada per l'increment.

En el GeoGebra la definició a trossos d'una funció s'ha de fer mitjançant el comandament condicional Si[]. ²⁾

La sintaxi és la següent:

• Si[condició, valor si es compleix la condició, valor si no es compleix la condició], que és una forma abreujada del comandament condicional If..else, o bé Si..altrament dels llenguatges de programació i que es correspon, fil per randa, amb el condicional dels fulls de càlcul.
• És important tenir present que dintre del valor si no es compleix la condició es pot emprar novament el comandament Si, cosa que caldrà aprofitar per definir una funció amb tres trossos o més, com la de l'exemple.
• Constateu que, si s'utilitza la idea dels llenguatges de programació, la definició de la funció és la següent:
  f(x) = Si x≤2 aleshores -4x+a
           altrament (que ja inclou -2<x)
                Si x<1 aleshores x²−5
                altrament b·x+3 (vegeu que s'aplicarà quan 1≤x)
           fi

Així doncs, per a l'elaboració de l'activitat, podeu procedir així:

• Definiu un punt lliscant que pugui variar de −10 a 10. Aquest serà el valor del paràmetre a.
• Definiu un altre punt lliscant, b, amb els mateixos límits de variació. Situeu els dos punts lliscants a la zona que us interessi de la pantalla.
• Ara escriviu a la zona d'entrada de comandes la definició de la funció d'acord amb les idees exposades:
  Si[x< = -2, −4x+a, SI[x<1, x²−5, b*x+3]]
  • Vegeu que el signe de més petit o igual es pot escriure amb els símbols < i = juxtaposats; també teniu el símbol al desplegable de símbols de la finestra d'entrada de dades. Vegeu també que el producte de b per x s'ha escrit amb el signe corresponent; es podria escriure també b x amb un espai per representar el producte, però no bx, perquè en aquest cas el GeoGebra entendria bx com el nom d'una nova variable.

Ja teniu la funció definida i dibuixada globalment, "tota de cop". Comproveu, per exemple, els valors f(0), f(5), f(-5). Observeu les variacions que es produeixen quan modifiqueu els valors dels dos paràmetres representats mitjançant els punts lliscants.

Per acabar la presentació de l'activitat tal com l'hem mostrat:

• Podeu modificar el gruix i el color de la funció.
• Podeu fer que es destaqui "on és" el punt de la funció en cada salt.
  • Escriviu A=(-2, f(-2))
  • Escriviu B=(1, f(1))
  • Podeu fer que no es mostrin les etiquetes dels punts i donar-los la mida i el color que convingui.

D'aquesta manera ja heu vist la possibilitat de definir funcions "a trossos" amb el GeoGebra. Sobre això convé comentar:

• Si la funció només té "dos trossos", la definició és més directa que l'exemple estudiat. Es farà amb un sol SI[].
• Tal com ho hem vist, la funció queda definida correctament i, a més, esdevé un element analític: podem calcular-ne directament la derivada o la integral, aspectes que es treballaran en el mòdul 6.

És interessant comentar una manera alternativa de mostrar una funció a trossos, aprofitant el comandament Funció[ ] que ja hem presentat anteriorment.

• Creeu com abans dos punts lliscants, a i b, amb valors de -10 a 10.
• Escriviu a la zona d’entrada Funció[-4 x + a, -200, -2]. Amb aquesta instrucció estem definint la funció -4 x + a des de -200 (que fa el paper del -∞, a efectes pràctics) fins a -2.
• Entreu a continuació les expressions que corresponen a les definicions dels altres trossos, a saber Funció[x²-5,-2,1] i Funció[b x + 3, 1, 200].
• Moveu els dos punts lliscants i observeu.

De la mateixa manera que hem fet servir els punts lliscants per assignar valors als paràmetres a i b que intervenien en la definició de la funció, també es pot definir una funció a trossos de manera que el(s) punt(s) de salt sigui(n) els valors d'un(s) punt(s) lliscant(s). Per si voleu experimentar (i preguntar dubtes, si escau) us proposem que busqueu amb el GeoGebra, mitjançant una funció definida a trossos amb l'ajut d'un punt lliscant, el valor de a que fa que la funció següent sigui contínua :
f(x) = x² − 1 si x ≤ a
         x + 5 si x > a.