Llocs geomètrics
lloc geomètric [MT] Conjunt de punts, generalment una línia o una superfície, que gaudeixen d’una propietat comuna.
La definició anterior la podem trobar al Diccionari de la Llengua Catalana (IEC). La gent d'una certa edat potser recorda una definició que van aprendre de memòria (en castellà, per l'època a què fem referència) quan eren menuts:
La circunferencia es el lugar geométrico de los puntos que equidistan de otro interior, llamado centro.
Certament aprendre coses de memòria no feia cap mal i, a més, creiem que aquesta definició concreta molt bé la idea de lloc geomètric: tots els punts (del pla) que tenen la propietat que estan a la mateixa distància d'un altre descriuen una circumferència.
Si volem estudiar quins punts compleixen una determinada propietat, hi haurà moltes vegades que escrivint-la a la línia d'entrada el GeoGebra ens mostrarà gràficament i analíticament el conjunt de punts que compleixen la propietat. Això serà possible quan la condició que determina el lloc geomètric es pugui escriure com una equació de segon grau.
Ara bé, en aquesta pràctica treballarem amb l'eina  Locus: Lloc geomètric que tenim al grup d'eines de rectes del GeoGebra, i convé dir que la idea de lloc geomètric associada a aquesta eina no és exactament la mateixa que la que acabem de comentar.
Locus: Lloc geomètric que tenim al grup d'eines de rectes del GeoGebra, i convé dir que la idea de lloc geomètric associada a aquesta eina no és exactament la mateixa que la que acabem de comentar.
El Locus del GeoGebra ens mostra la trajectòria que descriu un punt que és el resultat d'una construcció quan un altre punt que és objecte lliure en la construcció es mou al llarg d'un objecte.
En molts aspectes aquesta pràctica es pot considerar una proposta d'ampliació. De tota manera, és molt interessant que mireu els primers exemples per tenir una idea de com actua l'eina del locus o lloc geomètric i aleshores, si us ha interessat el tema, podeu estudiar l'apartat del pantògraf o el de l'el·lipse i us serviran com a exercicis.
Primers exemples
Una situació en què, amb el plantejament analític, el GeoGebra ens mostra de seguida la solució del problema, amb una eficàcia total, i, a més ens permet fer conjectures sobre aspectes més concrets de la solució.
* Si tenim dos punts A i B, quin és el lloc geomètric dels punts del pla amb la propietat que la distància a A és el triple que la distància a B?
Com es pot preparar la finestra anterior?
- Hem començat definint dos punts A i B.
- En el Geogebra no podem treballar directament amb un punt genèric (x,y) i, per tant, ens cal pensar analíticament.
- Hem escrit la condició de l'enunciat, després de recordar quina és la fórmula de la distància entre dos punts del pla i que sqrt( ) és l'arrel quadrada.
- L'enunciat es tradueix en sqrt( (x - x(A) )² + (y - y(A) )² ) = 3 sqrt( ( (x - x(B))² + (y - y(B))² ) ). El GeoGebra ens diu que no pot representar aquesta equació perquè no la pot operar per veure que és de segon grau.
- Hem escrit l'equació elevada al quadrat: (x - x(A))² + (y - y(A))² = 9 ( (x - x(B))² + (y - y(B))² ) i ja hem vist que el lloc geomètric solució del problema és una circumferència.
- Quan ja hem vist la solució, que ha quedat definida amb la letra c, hem fet servir la icona de Punt mitjà o centre, que ens ha dibuixat el centre de la circumferència solució i Radi[c] per saber-ne el radi.
Després hem escrit alguns textos, amb l'ús del comandament Distància[ ], i hem canviat el triple per k vegades per veure si conjecturàvem quin és el radi de c i la posició del seu centre, C, respecte A i B en un cas general. En aquesta feina ens pot ajudar el GeoGebra… però l'hem d'acabar nosaltres!
Com ja hem dit, l'eina locus o lloc geomètric del GeoGebra no es planteja exactament amb la idea dels llocs geomètrics conceptuals que acabem de veure. Tot seguit mostrem una situació, de la qual ja en sabem la solució, per explicar quin és el plantejament.
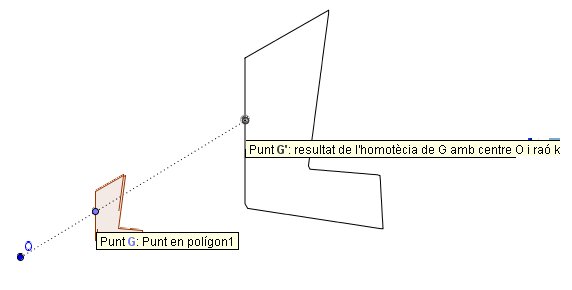
Experimenteu una mica en la finestra següent tot movent el punt G i observeu.
- Ja veieu que s'està emprant el traç d'un punt i així tenim idea de "com evoluciona" el punt G' a mesura que anem movent G pel contorn d'un polígon.
- També s'ha aplicat l'eina Locus: Lloc geomètric. El que fa aquesta eina és mostrar-nos "tot de cop" el traç d'un punt que té la propietat que es mou segons una determinada construcció; l'objecte resultant es mostra en funció de la posició del punt inicial.
La construcció (ara que ja hem passat l'equador del curs) és ràpida:
- Hem marcat el punt O.
- Hem definit el punt lliscant k que serà la raó d'homotècia.
- Hem posat No etiquetis objectes nous.
- Hem dibuixat el polígon i n'hem amagat els vèrtexs.
- Hem dibuixat un punt G sobre el polígon.
- Hem dibuixat el resultat d'aplicar al punt G l'homotècia de centre O i raó k. 1)
- No hem fet dibuixar el resultat d'aplicar l'homotècia al polígon. Això ho expliquem tot seguit.
Aleshores, si activem el traç de G i de G' tenim clara idea de quin serà el locus o lloc geomètric de G' quan es mogui G per tot el polígon.
També es pot fer, tot de cop, amb l'eina  :
:
- Feu Ctrl+f per esborrar el traç.
- Activeu l'eina indicada.
- Veureu que en l'ajuda d'aquesta eina diu: Seleccioneu un punt del lloc geomètric. Vol dir el punt G', el que volem veure com evoluciona.
- …i un punt d'una línia. Aquí hem de marcar el punt origen de la construcció, que ha de ser, forçosament, un punt sobre un objecte.2)
- Podríem substituir el treball amb l'eina per l'aplicació del comandament LlocGeomètric[G', G].
- I, si ho heu fet així, d'una manera o de l'altra, ja veureu dibuixat el conjunt de punts que recorre G' quan G es mou sobre el polígon.
Quan es dibuixa un locus, o lloc geomètric, s'obté un objecte especial, que s'actualitza si es modifica l'objecte original, que li podem donar propietats gràfiques personalitzades, que pot aparèixer en caselles de verificació… però que (de moment) no pot esdevenir objecte d'entrada per a eines geomètriques.
El pantògraf (*)
En aquest apartat, que podeu considerar d'ampliació, es mostra una activitat que sens dubte té una interessant aplicació didàctica: pot acompanyar una sessió de treball amb materials a l'aula, amb un pantògraf, un instrument mecànic que permet dibuixar figures homotètiques.
- A mesura que es mou un dels punts del pantògraf, totes les peces de l'instrument es mouen solidàriament tot mantenint una estructura de paral·lelogram.
- En un altre punt del pantògraf hi ha un aparell fixat que assenyala el traç del seu moviment.
Creiem que el pantògraf explica molt bé la idea del locus o lloc geomètric del GeoGebra. A mesura que nosaltres movem un punt, podem veure la línia que descriu un altre punt, de manera que es mantinguin sempre les propietats mecàniques que serveixen per construir l'objecte.
En veureu, en primer lloc, una mostra amb un alt grau d'acabat que simula peces de Meccano, l'explicació del qual escapa dels objectius d'aquest curs. Després s'explicarà l'elaboració d'un pantògraf lineal perquè, com ja hem dit, creiem que és un exemple interessant per comprendre què es fa quan s'aplica l'eina Lloc geomètric.
Per si voleu experimentar amb tot detall:
- El punt on el pantògraf està fixat es diu P, el punt on hi ha el llapis amb què dibuixem nosaltres es diu L, el punt on hi ha el punxó blau que escriu es diu E.
- Comproveu que P, L i E estan alineats.
- Comproveu que la raó de distàncies entre PE i PL és fixa, i és justament la raó d'homotècia que s'enuncia.
- Ja heu vist que el punt L es mou només sobre la figura "de la caseta" que és el polígon CC.
- Feu Ctrl+F per esborrar els traços que pugueu tenir, activeu l'eina del lloc geomètric i cliqueu primer a E i després a L. Oi que el pantògraf ens explica molt bé que fa aquesta eina? Ens dibuixa la línia que recorrerà E quan fem moure L per tot arreu on es pot moure.
- Si voleu "alliberar" el punt L podeu anar a actualitzar-ne les propietats i redefinir-lo, per exemple, com L=(0,0). Si us sembla, esborreu o amagueu la caseta… i ja podeu dibuixar lliurement i observar la imatge que construeix el pantògraf.
- Si voleu fer una altra figura (un altre polígon, un segment, una circumferència, una cònica…) i li poseu de nom FF, com es podria situar ràpidament el punt L sobre aquesta figura? N'hi hauria prou tornant a redefinir L com L=punt[FF].3)
Tot seguit s'explica com es pot fer la construcció en una versió esquemàtica que veieu en la figura següent (que no és una finestra activa).
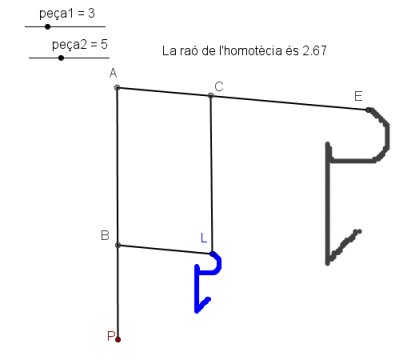
El pantògraf consisteix en una figura articulada construïda així:
- La figura base és un paral·lelogram ABLC.
- El costat AB forma part d'una peça sencera AP, de manera que BP = BL.
- Semblantment, el costat AC és part d'una peça rígida AE, de manera que CL=CE.
- El punt P es manté fix i esdevé el centre d'una homotècia en la qual el punt L es transforma en E.
- Per això, quan movem el punt L, s'observa que el punt E descriu una figura semblant a la que recorre L.
Per fer la construcció podeu procedir així:
- Definiu dos punts lliscants, c1 i c2, que representaran les mides, respectivament, de la peça que és el costat BL i de la peça que és el costat LC.
- Definiu el punt P, i feu que es mantingui sempre en el mateix lloc (Propietats | Fixa objecte).
- Definiu el punt L, que serà bàsic en la construcció.
- Circumferència de centre P i radi c1; circumferència de centre L i radi c1; el punt B es defineix a la intersecció d'aquestes dues circumferències. Podeu dibuixar ja el segment BL.
- Semirecta PB; circumferència de centre B i radi c2; la intersecció d'aquestes dues línies ens dóna el punt A. Podeu dibuixar el segment PA i aneu amagant objectes auxiliars.
- Per obtenir el punt C, que completa el paral·lelogram ABLC, ho podeu fer per paral·leles i esborrar línies auxiliars, o també vectorialment escrivint a la línia d'entrada: v = vector[B,L] (amagueu el vector v) i després C = A + v.
- Seguirem amb la mateixa idea vectorial per obtenir el punt E i així veureu una alternativa a la manera com hem obtingut A, que naturalment també serviria en aquest cas.
- Un vector de longitud 1 (dit versor) en la mateixa direcció i sentit que el vector v = AC = BL és el versor[v].
- El vector CE ha de tenir longitud c2. Serà c2*versor[v].
- Per tant, podeu definir E = C + c2*versor[v].
- Dibuixeu els segments AE i CL.
Ja teniu el pantògraf construït!
- Activeu el traç per als punts L i E i proveu si el pantògraf funciona.
- Acabeu tots els aspectes estètics tal com us agradi.
- I la raó d'homotècia, per si la voleu mostrar?
- No costa gaire demostrar raonadament que és (c1+c2)/c1. Podeu fer-ho així.
- Altrament també podeu anar a la definició de la raó d'homotècia i escriure-la com Distància[P,E]/Distància[P,L] i d'aquesta manera, de passada, comproveu que es manté constant.
Més amunt ja hem explicat com es pot fer per fixar ara el punt L a una figura, i després, si escau, per tornar-lo a "alliberar". Experimenteu-ho!
L'el·lipse com a lloc geomètric (*)
Presentarem dues activitats per reflexionar sobre la propietat que permet definir l'el·lipse com a lloc geomètric. L'objectiu és essencialment didàctic; no es presenten elements de treball nous del GeoGebra. Ara bé, si les voleu treballar, heu de saber que unes activitats anàlogues per a la hipèrbola en comptes de l'el·lipse serviran com un dels exercicis del mòdul.
Mireu la definició del diccionari de l'IEC:
el·lipse f. [MT] [LC] Corba plana closa que resulta de tallar la superfície d’un con de revolució per un pla que no és paral·lel a cap de les seves generatrius, els punts de la qual corba posseeixen tots la propietat que la suma de llurs distàncies a dos punts fixos o focus és constant.
- En la primera activitat comprovarem aquesta propietat.
- En la segona activitat visualitzarem l'el·lipse amb l'eina lloc geomètric.
Comprovació de la propietat definidora de l'el·lipse
Com sempre, podeu començar per experimentar en la pantalla següent, on teniu la primera d'aquestes dues activitats acabada i després explicarem com podeu dur a terme la construcció.
Es pot optar, per fer aquesta activitat, per construir l'el·lipse de qualsevol de les maneres que coneixem, amb les eines o els comandaments, però hem optat per fer-ho de la manera més general.
- Cliqueu sobre l’eina Cònica que passa per cinc punts.
- Cliqueu sobre 5 punts diferents de la zona gràfica, amb la intenció que aparegui una el·lipse i comproveu que automàticament es dibuixa una cònica c que passa pels cinc punts A, B, C, D i E. Si cal, moveu els punts de forma que la cònica sigui una el·lipse.
- Escriviu Focus[c] a la línia d'entrada i premeu Retorn. Es dibuixen els focus de la cònica; els anomena F i G, però podeu canviar el nom del segon per F'.
El següent pas és situar un punt P sobre la cònica i dibuixar els dos segments d i d' que uneixen el punt P amb els focus F i F':
- Utilitzant l'eina Punt nou apropeu-vos a la cònica, de forma que quedi seleccionada, i cliqueu. Es dibuixarà un punt sobre la cònica al qual canviareu el nom per P.4)
- Per assegurar-vos que P està sobre la cònica, utilitzeu l'eina Mou, arrossegueu el punt P i comproveu que P sempre es manté sobre la cònica.
- Utilitzant l'eina Segment entre dos punts cliqueu sobre P i sobre F, en qualsevol ordre, i obtindreu un segment al qual canviareu el nom per d.
- Repetiu l'operació anterior amb els punts P i F' i obtindreu un altre segment que anomenareu d'.
- Podeu veure que a la finestra algebraica apareixen els dos segments com a objectes dependents, i que el seu valor és precisament la seva longitud.
Finalment, posareu alguns rètols al tauler gràfic que mostrin que d + d' és constant, i aleshores, si escau, podeu amagar la finestra algebraica.
- Un dels que hem mostrat, ha de tenir això a la casella text:
"Es comprova que d + d' = " + (d + d') + "
per a tots els punts de l'el·lipse"
- Acabeu els altres textos i detalls de la presentació personalitzada com us sembli convenient.
Podeu provar la construcció movent el punt P sobre l'el·lipse i veient que, efectivament, d + d' es manté constant. Si tot funciona, guardeu la feina!
Construcció de l'el·lipse com a lloc geomètric
Tot seguit adoptarem un punt de vista diferent i, a partir de la propietat ja coneguda de la suma de distàncies als dos focus constant, construirem l'el·lipse amb l'eina del lloc geomètric.
- Es tracta de dibuixar una el·lipse donats el seu centre, O, un dels seus focus, F, i un dels seus vèrtexs principals, A.
- Com ja sabem, haurem de construir el conjunt dels punts del pla que tenen la propietat que la suma de les seves distàncies d i d' a dos punts F i F' (anomenats focus) és constant, d + d' = 2a, on a=Distància[O,A] sent O el centre de l'el·lipse, que és el punt mitjà de F i F'.
Podeu interactuar en la finestra activa següent. Són mòbils els punts definidors de la construcció, O, A i F i després el punt C per anar veient que el punt B i el punt D, que s'han definit a partir de la propietat de suma de distàncies, descriuen l'el·lipse com a lloc geomètric.
Indicacions per a la construcció:
- Els tres punts O, F i A han d'estar alineats sobre l'eix principal de l'el·lipse, per tant, començareu per dibuixar una recta i situar-hi els tres punts O, F i A; aprofitareu per situar també l'altre focus F'.
- Cliqueu sobre l'eina Recta que passa per dos punts i cliqueu sobre dos punts del tauler gràfic. Us apareixerà una recta que passarà pels dos punts A i B. Ja us va bé que un s'anomeni A, serà el vèrtex, però a l'altre, el B, com que voleu que sigui el centre, li canviareu el nom per O.
- Tot seguit, cliqueu sobre l'eina Punt nou, us situeu sobre la recta, entre el punts O i A, i dibuixeu un punt. Canvieu el nom d'aquest punt, sigui el que sigui, per F: serà el focus.
- Per dibuixar l'altre focus F', activeu l'eina Simetria central i seguidament, sobre F i O, per aquest ordre. Amb això, es dibuixarà el simètric de F respecte de O, l'altre focus; mireu que el nom d'aquest nou punt sigui F'.
- Finalment, observeu que la recta eix principal s'anomena a, i volem reservar la lletra a per la distància que apareix a la definició, és a dir el semieix major. Situeu-vos sobre la recta i canvieu-li el nom, per m o per eix, per exemple.
El següent pas és dibuixar punts de l'el·lipse, per poder veure com es faria punt a punt, o bé, en el nostre cas, veure-ho globalment amb l'eina lloc geomètric.
- Situeu un punt sobre l'eix principal, entre O i F, utilitzant l'eina Punt nou, i canvieu-li el nom per C.
- Definiu a la línia d'entrada els tres objectes següents:
- a = Distància[O,A]
- d = distància[F,C]
- d' = 2a - d.
- Cliqueu sobre l'eina Circumferència donats el centre i el radi; cliqueu sobre el focus F i, a la finestra que s'obrirà, escriviu d. Es dibuixarà una circumferència de centre F i radi d.
- Cliqueu de nou sobre l'eina Circumferència donats el centre i el radi; cliqueu ara sobre el focus F' i, a la finestra que s'obrirà, escriviu d'. Es dibuixarà una circumferència de centre F' i radi d'.
- Cliqueu sobre l'eina Intersecció de dos objectes 5) i seguidament, sobre les dues circumferències. Vigileu de fer-ho de manera que es defineixin els dos punts d'intersecció, B i D.
Observeu que els dos punts B i D són de l'el·lipse, perquè els hem construït de manera que:
- Distància[B,F] + Distància[B,F'] = d + d' = d + (2a - d) = 2a.
- Distància[D,F] + Distància[D,F'] = d + d' = d + (2a - d) = 2a.
Per donar idea ràpida de la construcció punt a punt, ho podem fer amb el traç activat.
- Situeu-vos sobre un dels dos punts B o D, cliqueu amb el botó dret del ratolí, aneu a Propietats i marqueu l'opció Activa el traç.
- Feu desprès el mateix amb l'altre punt.
- Si ara moveu el punt C sobre la recta eix principal, veureu com es mouen els punts B i D i van dibuixant l'el·lipse.
- Abans de continuar, amb Ctrl+F esborreu els traços i desactiveu l'opció Activa el traç dels dos punts B i D.
Per acabar veurem com podem dibuixar l'el·lipse aplicant dues vegades l'eina del locus o lloc geomètric.
- Trieu l'eina Lloc geomètric; si ho feu i, seguidament, cliqueu sobre B i C, per aquest ordre, es dibuixa el lloc geomètric que genera B quan es mou C (sobre l'únic lloc que es pot moure: sobre l'eix principal), és a dir, una semiel·lipse.
- Si torneu a utilitzar l'eina Lloc geomètric i cliqueu sobre D i C, es genera l'altra semiel·lipse.
Si tot ha anat bé, guardeu la feina, que amb la variació de l'el·lipse per la hipèrbola us pot servir per a un dels exercicis del mòdul… i per a l'ampliació que es comenta tot seguit.
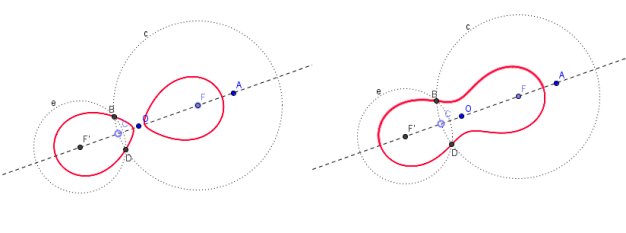
Els òvals de Cassini (*)
Els conjunts de punts amb la propietat que el producte de les seves distàncies a dos punts fixos és constant reben el nom d'òvals de Cassini. Una petita variació en la construcció anterior ens permetrà visualitzar aquestes corbes.
- Esborreu el lloc geomètric que definia l'el·lipse. 6)
- Situeu-vos a la finestra algebraica sobre l'objecte d'. Feu un doble clic amb el botó esquerre del ratolí i apareixerà un pop-up amb la casella Redefineix.
- Canvieu 2a - d per 2a/d i accepteu.
És clar que, tal com ho hem fet, els punts d'intersecció de les dues circumferències és el conjunt dels punts P del pla que tenen la propietat que el producte de les seves distàncies d i d' als dos focus F i F' és constant, d · d' = 2a.
- Segons les posicions de O, A i F pot passar que les dues circumferències no es tallin. Si us passa això, apropeu el focus F a l'altre focus F' usant l'eina Moure.
Aleshores torneu a definir el lloc geomètric de B en funció del moviment de C, i semblantment per al lloc geomètric de D. Veureu que apareix l'òval.
Experimenteu per constatar que, segons les posicions dels punts bàsics de la construcció, pot aparèixer una corba amb dues fulles no connexes o també amb una sola fulla.
Vegeu dues imatges d'aquestes corbes que reben el nom d'òvals de Cassini.