Polígons regulars, "regulars" i estrellats
Ja sabeu que no tots els polígons regulars són construïbles amb regle i compàs. En aquesta pràctica veurem la construcció clàssica del pentàgon regular (és a dir, fent servir les eines de rectes i circumferències del GeoGebra).
Tanmateix, en els textos de dibuix de l'ESO es presenten construccions de polígons "regulars" que, tot i que són aproximades, algunes són molt acurades. En veurem una i constatarem que, per a molts efectes pràctics, potser no cal portar el rigor a l'extrem.
El GeoGebra té l'eina Polígon regular que dibuixa directament un polígon regular de n costats a partir de dos vèrtexs consecutius; ja l'hem fet servir en pràctiques anteriors. És clar que el treball intern del programa fa servir l'analítica i la trigonometria; també és clar que la construcció no és "exacta"… però el grau d'aproximació és difícilment superable.
Hi ha dues altres situacions de construcció analítica de polígons regulars per a les quals el GeoGebra no té un comandament. A saber:
- La construcció d'un polígon regular inscrit en una circumferència, per a la qual farem una macro amb l'ajut de llistes.
- La construcció d'un polígon regular coneguts el centre i un vèrtex (que quedarà com a exercici).
Acabarem la pràctica canviant una mica la macro que hem comentat per poder dibuixar polígons estrellats.
El pentàgon regular
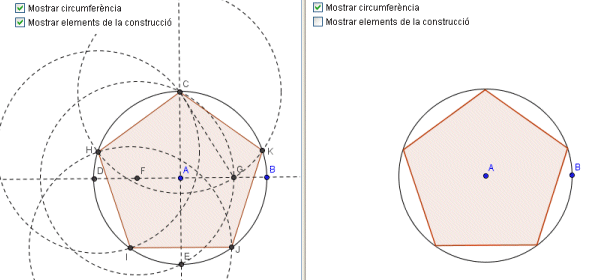
Si a la finestra següent cliqueu al botó  , o bé aneu fent la reproducció de la construcció pas a pas clicant sobre el botó
, o bé aneu fent la reproducció de la construcció pas a pas clicant sobre el botó  , tindreu una idea molt clara de l'activitat que es vol fer en aquest apartat: una de les construccions que feien els geòmetres grecs del pentàgon regular.
, tindreu una idea molt clara de l'activitat que es vol fer en aquest apartat: una de les construccions que feien els geòmetres grecs del pentàgon regular.
Construcció
- Amb l'eina Punt nou dibuixeu els punts A i B.
- Amb l'eina Circumferència donats el seu centre i un punt per on passa, dibuixeu una circumferència amb centre en A i que passi per B. Serà la circumferència on inscriureu el pentàgon regular.
- Amb l'eina Recta que passa per dos punts dibuixeu la recta AB.
- Amb l'eina Recta perpendicular, clicant sobre el centre A i sobre la recta AB, dibuixeu una recta perpendicular a AB pel centre A de la circumferència.
- Amb l'eina Intersecció de dos objectes trobeu les interseccions C, D i E de la circumferència i les dues rectes anteriors. C serà un vèrtex del pentàgon.
- Amb l'eina Punt mitjà o centre dibuixeu el punt mitjà F del radi AD.
- Amb l'eina Circumferència donats el seu centre i un punt per on passa dibuixeu una circumferència amb centre a F i radi FC.
- Amb l'eina Intersecció de dos objectes trobeu la intersecció G de la circumferència anterior amb el radi AB. És sabut que el costat del pentàgon regular és CK.
- Amb l'eina Circumferència donats el seu centre i un punt per on passa dibuixeu una circumferència amb centre a C i radi CG.
- Amb l'eina Intersecció de dos objectes trobeu la intersecció H de la circumferència anterior amb la primera circumferència. H és un altre vèrtex del pentàgon.
- Repetiu els dos passos anteriors dues vegades més per obtenir els vèrtexs I i J. Per obtenir el vèrtex K no cal dibuixar més circumferències, n'hi ha prou de trobar la intersecció de dues ja existents.
- Amb l'eina Polígon cliqueu successivament sobre C, H, J, I, K i C per obtenir el desitjat pentàgon regular.
Podeu ocultar tots els elements de la construcció tret del pentàgon o, alternativament, pot ser convenient posar una casella de verificació que els mostri/amagui donant, si ho creieu convenient, un tractament especial a la circumferència.
És un heptàgon regular? (*)
Vegeu les indicacions que teniu tot seguit per a la construcció de l'heptàgon regular que s'explica en alguns textos d'ESO (matèria de Visual i Plàstica).
- Dibuixa una circumferència de centre A i traça un diàmetre AB.
- Fes la mediatriu del segment AB.
- Si M és el punt mitjà de AB i E és el punt on la mediatriu talla la circumferència, aleshores EM és el costat d'un heptàgon regular.
Ho vam fer així i després, a partir del vèrtex E, vam anar situant per circumferències segments iguals a EM i ens va sortir el dibuix següent.
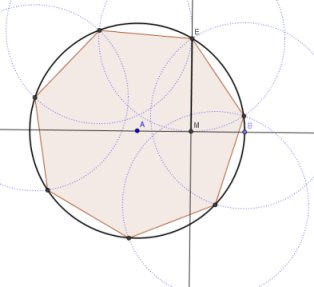
És realment un heptàgon regular?
No! Sabem que l'heptàgon regular no és construïble amb regle i compàs, per tant tampoc no el podrem construir amb el GeoGebra si només utilitzem eines de rectes i circumferències. Però, a primer cop d'ull, ho sembla! És una acceptable construcció aproximada1), molt eficaç, per la seva senzillesa, en moltes situacions pràctiques.
Polígons regulars
Ja heu emprat repetidament, en pràctiques anteriors, l'eina Polígon i també l'eina Polígon regular que ens dibuixa un polígon regular donant-ne dos vèrtexs consecutius i el nombre de costats. No és una construcció de la geometria clàssica però segur que és més exacta que qualsevol altra que poguéssim fer amb regle i compàs, fins i tot per als polígons construïbles. El dibuix amb ordinador ha fet canviar moltes idees de cara a les aplicacions pràctiques.
Com hem fet per a altres comandaments, comentem ara breuement les possibilitats per construir polígons i polígons regulars des de la línia d'entrada:
- Si posem com a arguments a la comanda Polígon[ ] una successió de punts, Polígon[
punt, punt, punt,…], es crea el polígon que té per vèrtexs els punts indicats. - Si en canvi indiquem com a arguments dos punts i un nombre, Polígon[
punt, punt, nombre], aleshores aquest comandament equival a l'eina Polígon regular clicant en els dos punts indicats i donant-li el nombre de costats adient. Vegeu, doncs, que la comanda no és Polígon_regular[ ] sinó Polígon[ ] amb els arguments adequats.
Però moltes vegades no és aquesta situació, la de conèixer dos vèrtexs consecutius, la que interessa quan volem construir un polígon regular.
Ara dissenyarem una eina que permeti dibuixar un polígon regular inscrit en una circumferència, clicant sobre la circumferència i sobre un punt de la circumferència que serà "el primer" vèrtex i donant, naturalment, el nombre de costats.
Per definir aquesta macro, ho podeu fer així:
- Engegueu el GeoGebra. No cal que es vegin els eixos ni la graella. És recomanable que l'opció pel que fa a les etiquetes sigui no etiquetar objectes nous.
- Per definir una circumferència, i que sigui un objecte fix mentre preparem la macro, pot ser interessant definir-la mitjançant una equació.2) Escriviu, per exemple, a la casella d'entrada de comandes, x2 + y2 = 8. Segur que GeoGebra li posa per nom c.
- Trieu l'eina Punt mitjà o centre i després cliqueu sobre la circumferència. N'haurà quedat marcat el centre; per seguir millor l'explicació següent imaginem que li canviem el nom i li posem C.
- Marqueu un punt sobre la circumferència i procureu que tingui per nom A.
- Definiu un punt lliscant, que li posarem per nom n, increment de variació 1 perquè prengui valors enters i límits de variació, per exemple, de 3 a 25.
Ja tenim preparats tots els elements per escriure una comanda seqüència que generarà els vèrtexs d'un polígon regular de n costats, inscrit en la circumferència c i que té com un dels seus vèrtexs el punt A. Entre les maneres diverses que tenim de generar aquest polígon, ara suggerim de fer-ho per rotacions successives del punt A amb centre en el de la circumferència i angles de 360°/n.
- Recordeu que la comanda Rotació té la sintaxi Rotació[element a girar, angle, centre] i aleshores entreu
LLV = Seqüència[ Rotació[A,i*360°/n,C], i, 0, n] amb ° triat en el desplegable corresponent.3)
D'aquesta manera feu una llista que, a més de tenir els punts que defineixen el polígon regular de n costats, comença i acaba en el punt "llavor".4) Això ho hem fet així perquè tot seguit passarem a dibuixar els segments que constitueixen els costats del polígon regular.
- Per dibuixar els costats del polígon regular hem d'unir cada vèrtex amb el següent, és a dir l'element i de la llista anterior amb l'element i+1. Així:
LLS = Seqüència[ segment[Element[LLV,k], Element[LLV, k+1]], k, 1, n].
Ja haureu vist definit el polígon regular de n costats. Feu proves i canvis per veure que funciona i, en cas que sigui així, anem per definir la macro.
- Objectes de sortida: la llista LLV (llista de vèrtexs) i la llista LLS (llista dels segments que constitueixen els costats del polígon).
- Objectes d'entrada: la circumferència C, el punt A sobre la circumferència i el numèric n. Vigileu que el valor numèric es demani com a darrer objecte d'entrada.
Comproveu que la macro funciona. Pot ser interessant fer-ho amb circumferències construïdes de maneres diverses (per a l'equació, circumferència que passa per tres punts, circumferència donat el centre i el radi…) i veure que la macro sempre actua correctament. Després pot ser interessant esborrar tots els elements que han servit per fer comprovacions que la macro funciona; tanmateix, no esborreu els objectes fonamentals, els que han servit per dissenyar-la: hi continuareu treballant. Si tot va bé, guardeu la feina; pot ser interessant que enregistreu la macro com a tal, amb un fitxer .GGT (recordeu: Eines | Administra les eines | Anomena i desa).
Potser preguntareu: què hauríem de fer perquè també s'acolorís, en la macro anterior, la superfície del polígon? Us ho deixem com a tema obert per a la investigació!
Polígons estrellats (*)
Podríem començar la feina de cap i de nou, però aprofitarem les llistes que ja tenim, la de punts i la de segments, perquè, redefinint-les, ens serviran per dibuixar polígons estrellats. Volem que elaboreu una activitat com aquesta:
- Teniu un punt lliscant n, que varia de 3 a 25, que indica el nombre de vèrtexs que tindrà el polígon. Ara volem un altre valor numèric que indiqui "de quants en quants" volem unir els vèrtexs, que ens interessa que variï de 1 a n - 1. Tanmateix, amb el GeoGebra5) els límits dels punts lliscants han de ser nombres fixos. Ara expliquem un petit artifici per aconseguir obtenir, amb l'ajut d'un punt lliscant, un valor numèric p que prengui valors enters de l'interval [1, n-1].
- Definiu un nou punt lliscant q i feu que variï de 1 a 25, amb increment 1. Feu que no es mostri l'etiqueta d'aquest punt lliscant.
- A la casella d'entrada de comandes definiu un altre valor p així:
p = Si[q<n, q, n-1]
Com veieu, p prendrà el valor que indica el punt lliscant q mentre sigui menor que n, però si el punt lliscant té com a valor n o més, aleshores el nou valor numèric p no passarà mai de n-1. - Creeu un text que digui
"p = " + pi situeu-lo com si fos l'etiqueta del punt lliscant q.
- Redefiniu la llista de punts així:
LLV = Seqüència[ Rotació[A,i*360°/n,C], i, 0, n*p]
D'aquesta manera tindrem una llista de possibles vèrtexs que dóna p voltes a la circumferència. - Per dibuixar els costats del polígon estrellat (que també pot ser que no resulti estrellat, com ja haureu vist si heu fer proves en la finestra activa que hem adjuntat) hem dit que volem unir els vèrtexs "de p en p", és a dir, començant pel vèrtex 16), del vèrtex 1 al vèrtex 1+p; després del 1+p al 1+2p; seguirem del 1+2p al 1+3p i així successivament; com que volem dibuixar n costats, el darrer segment a considerar serà el que va del vèrtex 1+(n-1)p al vèrtex 1+np.7) Redefiniu, doncs, la llista de segments com s'indica seguidament:
LLS = Seqüència[segment[Element[LLV,1+k*p], Element[LLV, 1+(k+1)*p]], k, 0, n-1] - I ja només falta, si voleu, que feu el rètol explicatiu de l'activitat.
Comproveu que tot funciona i guardeu la feina! Segur que amb aquesta macro ja podeu investigar (o, encara millor, fer investigar l'alumnat) quants vèrtexs apareixen, efectivament, en un polígon estrellat (o no) obtingut a partir de n vèrtexs d'un polígon regular inscrit en una circumferència que unim de p en p.
Oi que, tot i que el treball amb llistes sigui un recurs avançat, sembla que val la pena interessar-se pel seu funcionament?

