Tangències i altres problemes de geometria

Seguint la idea del títol del mòdul, Fem Geometria, en aquesta pràctica es presenten quatre problemes que es resolen amb l'ajut de les eines de geometria del GeoGebra.

• Per saber la longitud d'una ombra ens cal treballar les tangents a una circumferència des d'un punt exterior.
• En el segon estudiarem les tangents a una el·lipse i una hipèrbola.
• El tercer farà ús de les rotacions per construir un triangle equilàter que es recolza en tres rectes paral·leles donades.
• En el quart veurem que un ús acurat de les translacions ens pot ajudar a saber on s'ha de construir un pont.

A prop d'una paret hi ha una columna i, a l'altre costat de la columna, un focus lluminós. Volem calcular l'amplada de l'ombra que el focus lluminós fa a la paret.

Ja veieu a la imatge que caldrà fer servir l'eina Tangents per traçar les dues rectes tangents a un circumferència des d'un punt exterior. Després s'han d'obtenir les interseccions de les tangents amb una altra recta i la distància entre aquestes dues interseccions.

Hem fet un estudi previ per mirar d'enfocar el problema analíticament, amb l'ajut del GeoGebra, i l'hem pogut reformular així:
Una columna circular d'1 m de radi està centrada en l'origen de coordenades, hi ha un focus lluminós puntual al punt (-5,-5) i una paret a la recta x+y = 6. Calculeu l'amplada de l'ombra que la columna fa sobre la paret.

A la finestra següent teniu el resultat de la pràctica; fent doble clic a l'interior podeu accedir a una finestra GeoGebra completa.

Per l'enfocament analític que hem fet del problema, és convenient treballar amb eixos, graella i finestra algebraica visibles.

Dibuixeu primer tots els elements del problema:

• Un punt en (-5,-5): escriviu P = (-5,-5) a la casella d'entrada i feu Retorn.
• Una circumferència centrada a l'origen de radi 1: utilitzeu l'eina Circumferència donats el centre i el radi, cliqueu sobre l'origen de coordenades, s'obrirà una finestra demanant el radi, hi poseu radi = 1 i accepteu. Alternativament, podeu escriure a la línia d'entrada x² + y² = 1.
• La recta x + y = 6: n'hi ha prou amb escriure x + y = 6 a la casella d'entrada i prémer Retorn.

Traceu les tangents a la circumferència per P:

• Utilitzeu l'eina Tangents, cliqueu sobre el punt P i sobre la circumferència; es traçaran les dues tangents.

Obtingueu les interseccions de les dues rectes anteriors amb la recta x + y = 6:

• Utilitzeu l'eina Intersecció de dos objectes; cliqueu sobre una recta tangent i sobre la recta x + y = 6; repetiu el procés amb l'altra recta tangent.

Calculeu la distància entre les dues interseccions anteriors. Hi ha diverses maneres de fer-ho, per exemple:

• Utilitzar l'eina Segment entre dos punts. Si cliqueu sobre els dos punts d'intersecció, es dibuixa aquest segment i, a la finestra algebraica, surt la seva longitud: e = 3.23, per tant, l'amplada de l'ombra és de 3,23 metres.
• Utilitzar l'eina Distància. Cal clicar sobre les dues interseccions i la distància també apareix com a objecte numèric a la finestra algebraica.
• Amb el comandament Distància[B, C] (si B i C són els noms dels dos punts d'intersecció, com a la finestra que us hem mostrat).

Finalment, entrant a Propietats, podeu canviar colors, estils de línia, activar o desactivar etiquetes… També podeu amagar o visualitzar la finestra algebraica.

En la finestra activa següent podeu veure una el·lipse i una hipèrbola que tenen els mateixos eixos i hi ha dibuixades les tangents a les dues còniques en un dels punts d'intersecció. Hi ha alguna posició especial dels focus de les dues còniques, o algun valor de les excentricitats, que faci que les tangents siguin perpendiculars?

• Imaginarem que els eixos comuns són els de coordenades i, per tant, l'origen de coordenades serà el centre de les còniques.
• Marqueu un focus E de l'el·lipse i, amb l'eina Simetria central, feu el simètric respecte a l'origen de coordenades, que serà E'.
• Amb l'eina El·lipse dibuixeu una el·lipse que tingui aquests dos focus i passi per un punt A.
• Feu el mateix per a una hipèrbola de focus H i H' i que passi per B.
• Ara marqueu un dels punts comuns a l'el·lipse i la hipèrbola, P.

Per traçar les tangents:

• Fareu servir l'eina Tangents i observareu que si marqueu l'el·lipse i un punt de la corba, P, es dibuixa correctament l'única tangent que hi ha en aquest cas.
• Feu el mateix per a la hipèrbola.

Per marcar l'angle:

• Teniu l'eina Angle. Cliqueu a les dues rectes en l'ordre adequat per visualitzar l'angle que voleu.

• Podeu variar els focus de cada cònica si moveu els punts E o H.
• Podeu variar l'excentricitat de cada cònica si, mantenint-ne fixos els focus, moveu l'altre punt que les defineix, A o B.

Heu aconseguit una posició en la qual les tangents siguin perpendiculars?¹⁾

Donades tres rectes paral·leles es demana construir un triangle equilàter que tingui un vèrtex en cada una de les rectes. Aquest problema té sempre solució, sigui quina sigui la distància entre les rectes?

Si imagineu el problema resolt, veureu que un dels vèrtexs es pot fixar lliurement; és l'O de la finestra activa següent. Moveu les rectes per veure si descobriu la manera de resoldre el problema i decidiu si sempre té solució o no.

• Dibuixem les tres rectes paral·leles, a, b, c.

Ara imaginem el problema resolt, amb les lletres que teniu a la finestra anterior.

• Ja hem dit que el punt O el podem posar lliurement en un punt d'una de les rectes.
• La solució del problema rau en observar que el punt E resulta d'una rotació antihorària de centre O i angle 60º del punt D.
  • Per aquesta raó, si fem una rotació antihorària²⁾ de 60º de la recta a, el punt d'intersecció de la recta transformada amb b serà el punt E.
            

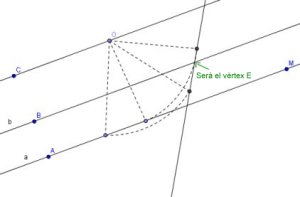
• Una vegada situat el punt E, sabem que aquest és la imatge del vèrtex D per a una rotació antihorària de 60º de centre O. Per tant, amb la transformació recíproca, trobarem D amb una rotació horària³⁾ de E d'angle 60º.
• I amb això ja hem acabat el problema.
          

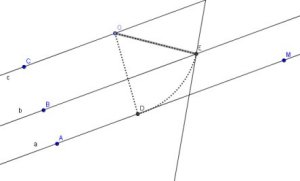
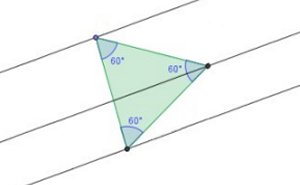
Podeu veure que sempre que comencem amb tres rectes diferents el problema té solució.

Tot seguit es planteja un problema d'optimització i se'n mostra una solució de geometria constructiva. És un bon exemple, de clara utilitat didàctica, per a explicar la utilitat de l'aplicació dels recursos geomètrics a situacions pràctiques, sense necessitat de recórrer, com moltes vegades sembla "indispensable", a mètodes de l'anàlisi matemàtica.

Podreu comprovar que la finestra activa de GeoGebra que teniu tot seguit no es pot obrir separadament de la pàgina web, així com en d'altre ocasions es poden obrir fent doble clic sobre la construcció en aquest cas està "tancada" expressament.

Si la visualitzeu a la pantalla anterior entendreu que si fem una translació del punt A amb un vector igual al que va del començament al final del pont i unim el punt resultant amb B, la intersecció d'aquesta recta amb la segona riba del riu ens indica "on ha d'acabar" el pont i, per tant, ja tenim resol el problema.

Només esquematitzarem els passos de la construcció perquè, com ja s'ha dit, podeu triar l'acabament acurat d'aquesta construcció com un dels exercicis del mòdul.

• Tot i que en la situació real naturalment "primer seria el riu i després el pont", com que ens basarem en una figura del pont per fer la construcció, convindrà començar pel pont…:
  • Aquí teniu la imatge del pont:
    
    Ja sabeu que amb el botó dret i Anomena i desa la imatge podeu descarregar-la al vostre ordinador. Després importeu-la cap al GeoGebra i poseu-la en un punt de la pantalla per on passarà el riu.
  • Situeu també d'antuvi a la pantalla les dues poblacions, és a dir els punts A i B.
    

• …i després anirem dibuixarem el riu:
  • Marqueu dos punts M i N que assenyalin els extrems del pont. Es podria fer en funció de Cantonada[ ] de la figura com es va explicar en alguna altra pràctica, però també els podem situar "a mà". ⁴⁾
  • Definiu el vector v que uneix els punts M i N.
  • Com que el riu haurà de ser perpendicular a aquest vector, convé considerar ara el vector u = VersorPerpendicular[v] que és un vector de mòdul 1 perpendicular a v.
  • Amb aquest vector com a ajut no us serà difícil construir un paral·lelogram, que escapi de la pantalla, que representarà el riu. Pinteu-lo de color blau amb ombrejat del 100%!
  • Ha tapat el pont!, direu!
    Efectivament. Convé que aneu a les propietats del pont, del punt M i del punt N, i a la pestanya Avançat poseu que estiguin a la Capa 1, que queda per davant de la capa on es dibuixen les figures per defecte, que és a la capa 0. Però a partir d'ara ja es dibuixaran totes a la capa 1.
    
  • Com que u i v ja els teniu in mente, els podeu amagar.

• Per moure el pont de manera que es mantingui sempre perpendicular al riu i sense separar-se'n de les riberes, farem una translació de vector perpendicular al pont, és a dir múltiple de u. Variarem el mòdul d'aquest vector de translació amb un punt lliscant.
  • Definiu un punt lliscant k i deixeu que variï, com ens proposa el programa, de -5 a 5.
  • Definiu un vector vt = k * u , que de moment veureu a la pantalla.
  • Cliqueu a la icona de la transformació geomètrica Translació segons un vector.
    • En primer lloc, amb la icona de translació activa, marqueu un rectangle que abasti el pont, que ja agafarà també els punts M i N.
    • Cliqueu ara sobre el vector vt, cosa que podeu fer allà on ha quedat dibuixat o al vt de la finestra algebraica.
  • Comproveu que movent el punt lliscat efectivament el pont es trasllada com volem que es traslladi i que hi queden dibuixats, solidàriament, uns punts M' i N' que en marquen els extrems.

• Ara convé amagar el pont original i els punts M i N. Tranquils!, que encara que amagueu el pont, el traslladat, que és el que interessa perquè és l'indret per on ha de passar la carretera, es seguirà veient. També podeu amagar el vector vt.

• Ara dibuixeu la carretera i feu que se'n calculi la longitud.
  • Heu de dibuixar tres segments, que ja podeu fer gruixuts i de color gris!
  • Ja sabeu que amb la lletra identificadora de cada segment, a la finestra algebraica se'n mostra la seva longitud. És bo saber que aquesta lletra identificadora també actua com un valor numèric. Si els tres segments es diuen s₁, s₂ i s₃, aleshores podem escriure a la línia d'entrada long = s₁+s₂+s₃ i tindrem la longitud total de la carretera.
    

• Ja podeu anar enllestint tots els aspectes estètics, rètols, etc…

• Ui! Queda per fer l'explicació de com es troba la solució…

Aquesta tasca ja us la deixem a vosaltres! Bona feina!