Correlació i regressió

Una de les novetats que ha incorporat la versió 3.2, abril de 2009, és la possibilitat de fer una anàlisi estadística bivariant a partir d'un conjunt de dades. Aquesta anàlisi es concreta en l'estudi de la correlació lineal i en l'aplicació d'un model de regressió adequat que ens permeti fer determinades prediccions. En aquesta pràctica veureu uns exemples que il·lustraran les diferents possibilitats del GeoGebra en aquest camp de l'Estadística.

Comencem per la part més senzilla. El GeoGebra actual incorpora una eina que resulta molt fàcil d'utilitzar si el que es vol és trobar directament la recta de regressió d'un núvol de punts entrats directament amb el ratolí. El resultat pot ser semblant a:

Desplaceu qualsevol dels punts i observeu com va variant la recta de regressió. La construcció és molt fàcil:

• Feu que no surti cap etiqueta.
• Entreu uns quants punts a la zona gràfica de la manera habitual.
• Seleccioneu l'eina Recta de regressió.
• Amb el botó esquerra del ratolí premut, seleccioneu els punts traçant un rectangle de selecció com es veu a la figura.

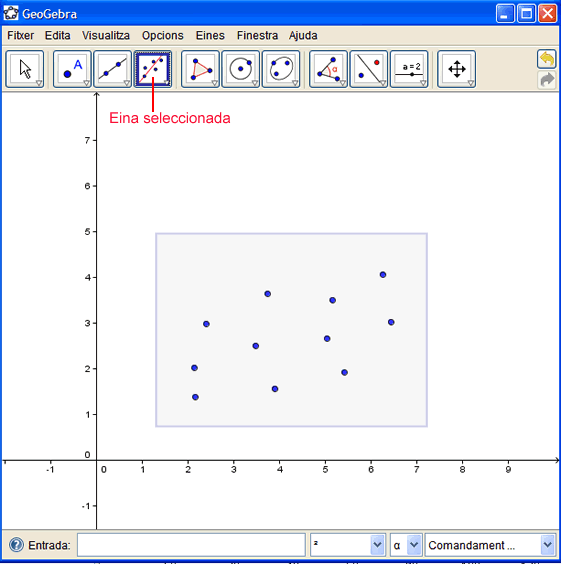
• Deixeu anar el botó i ja apareixerà la recta de regressió.
• Accediu a la seva expressió, que trobareu a la finestra algebraica, i, amb el botó dret del ratolí, trieu l'opció Equació y = ax + b.

Tot seguit podeu entrar el text variable que es veu i els altres detalls estètics. Com podeu veure, el procediment és molt senzill.

En aquest exemple anterior no heu calculat el coeficient de correlació lineal ni cap altre paràmetre estadístic. Ara veureu com el full de càlcul ens pot anar bé per aprofundir més en l'anàlisi.

Suposem que un grup de 14 alumnes passen un examen i uns mesos després tornen a passar una prova similar. Volem estudiar la relació que hi ha entre les dues proves i si podem assegurar si els resultats són millors o no.

En aquesta finestra activa teniu el núvol de punts dibuixat a partir de les notes obtingudes en els dos exàmens.

Si activeu la casella de verificació Paràmetres, veureu les mitjanes i desviacions estàndard de cada variable, el coeficient de correlació lineal r i l'expressió de la recta de regressió.

Si activeu la casella de verificació Eixos punt mitjà, apareix el punt mitjà del núvol de punts, és a dir, el punt que té per coordenades les mitjanes de cada variable, i uns eixos que tenen per origen aquest punt mitjà. Aquests eixos van molt bé per analitzar el signe del coeficient de correlació lineal en funció dels punts del núvol que queden en cada quadrant i la seva llunyania del punt mitjà.

Si activeu, ara, la casella de verificació Recta, teniu a la vista la recta de regressió. Observeu que passa pel punt mitjà i que, en aquest cas, és creixent. També apareix una nova casella de verificació anomenada Prediccions.

Si teniu activades les caselles Recta i Prediccions, podeu analitzar, seguint el model de la recta regressió calculada, quina nota hauríem d'esperar en la segona prova per a cada nota de la primera. Així, desplaceu el punt que està situat a l'eix horitzontal i que només es podrà moure a l'interval [0,10], i observeu la seva imatge a l'eix vertical. Cal tenir present que les prediccions només tenen sentit si volem inferir els resultats obtinguts d'una mostra cap al conjunt de la població. Per tant, hem d'imaginar que aquests/es alumnes han estat escollits/des a l'atzar d'un col·lectiu més gran i que, per tant, la recta de regressió serveix com a model per predir quina segona nota podem esperar d'un/a alumne/a qualsevol d'aquest col·lectiu, a partir de la seva primera nota.

Amb aquesta construcció, l'alumnat pot observar i manipular els seus elements per treure conclusions interessants. Us avancem algunes preguntes que es podrien fer:

• Quin dels exàmens ha anat millor? Quins paràmetres t'ho indiquen?
• Quin tipus de correlació lineal s'observa amb aquestes dades?
• Desplaceu un sol punt per aconseguir que el coeficient de correlació lineal sigui molt petit. Quin tipus de correlació lineal tenim ara amb aquest canvi?
• Desplaceu un altre punt per aconseguir una correlació lineal inversa. Valoreu la importància de la posició de pocs punts en determinats quadrants dels eixos del punt mitjà.
• Torneu a la situació inicial i activeu Rectes i Prediccions. Quines notes es podrien esperar a la segona prova per a notes molt baixes de la primera si seguim el model d'aquest recta de regressió? I si la nota de la primera prova és molt alta? Comenta el que observes. Creus que aquest efecte el pots trobar en altres situacions?

Com s'ha fet aquesta construcció? Seguiu les indicacions següents per arribar-hi.

• Entreu les dades de les columnes A i B. Són les notes obtingudes a cadascuna de les proves.

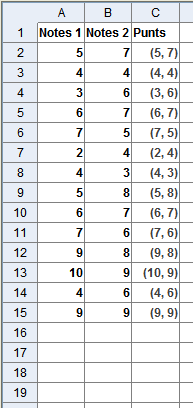
• Feu que no surtin les etiquetes de cap objecte.

• Entreu a la cel·la C2 l'expressió (A2,B2) i copieu-la, arrossegant el petit quadrat blau columna avall fins a arribar a la cel·la C15. A la zona gràfica ja ha aparegut el núvol de punts.

• Seleccioneu el rang C2:C15 i, amb el botó dret, trieu l'opció Crea llista. S'haurà creat una llista de punts anomenada L₁.

A partir d'aquest núvol de punts i d'aquesta llista, podeu trobar:

• La recta de regressió. Trieu l'eina Recta de regressió i seleccioneu el núvol de punts com en l'apartat anterior.
• El coeficient de correlació lineal amb el comandament r=CoefCorrel[L_1].
• Les mitjanes de cada variable amb xx=Mitjana[A2:A15] i yy=Mitjana[B2:B15].¹⁾
• Les desviacions estàndard de cada variable amb dx=DesviacióEstàndard[A2:A15] i dy=DesviacióEstàndard[B2:B15].
• El punt mitjà de la distribució de dades amb PM=(xx,yy).
• Els eixos del punt mitjà dibuixant rectes perpendiculars als eixos de coordenades que passin per PM.

A continuació, creeu els elements per fer les prediccions.

• Creeu un segment que vagi del punt (0,0) fins al punt (10,0).
• Creeu un punt que estigui situat sobre el segment anterior. D'aquesta manera no podrà sortir de l'interval [0,10], que és el rang de les notes possibles.
• Ara cal fer les perpendiculars (o paral·leles) als eixos, les interseccions i els segments fins arribar a visualitzar la imatge del punt inicial.

Ara només queda entrar els textos i definir correctament les caselles de verificació. Recordeu que la casella Prediccions només s'ha de veure si està activada la casella Recta. Per això, haureu d'entrar el nom de la variable booleana de Rectes com a condició per mostrar-la, procediment que ja heu fet servir en altres pràctiques.

Acabeu amb els detalls estètics i guardeu la feina.

En aquest apartat veureu com podeu estudiar la correlació lineal de determinades subpoblacions que poden trobar-se dins d'una població més gran. Aquí en teniu un exemple:

Us aconsellem que feu un doble clic sobre la finestra per poder ampliar-la i veure millor els detalls. Observeu que segons quina sigui la casella activa veureu un núvol de punts diferent amb un coeficient de correlació lineal i una recta de regressió propis. Aprofiteu aquesta acció per recollir les dades que trobareu al full de càlcul.

Per a la construcció, heu de tenir en compte el següent:

• Heu de seleccionar el rang B2:C36, és a dir les altures i els pesos del homes, i amb el botó dret trieu l'opció Crea llista de punts. Aquesta és una manera de crear un llista de punts directament sense haver d'escriure'ls al full de càlcul. Aquesta serà la llista anomenada llista1.
• Feu el mateix amb les altures i els pesos de les dones. Haureu generat la llista2.
• Executeu el comandament Concatena[{llista1, llista2}]. D'aquesta manera es generarà la llista3 com a unió de les dues llistes anteriors.
• Doneu els colors indicats per identificar millor els diferents núvols de punts.
• Calculeu els coeficients de correlació lineal i la recta de regressió per a cada llista. Podeu fer servir el comandament RegLineal[nom de la llista] amb la llista adequada per a cadascuna de les rectes.
• Els textos explicatius han d'estar situats al mateix lloc i han d'associar-se a cada casella de verificació.

Estem segurs que no tindreu cap dificultat per fer la construcció. Ja sabeu que en cas de dubte podeu fer consultes a la tutoria.