El full de càlcul de GeoGebra

Una de les novetats de la versió 3.2 és la incorporació d'un full de càlcul. Fins ara no hi hem treballat, però el vam presentar en les primeres pràctiques.

• Recordeu que per accedir-hi, ho podeu fer a partir el menú Visualitza | Full de càlcul, o bé amb la combinació de tecles Ctrl+Shift+R.

Com tots els programaris de full de càlcul, el del GeoGebra estructura la informació en files i columnes. Cada cel·la té per nom la lletra, amb majúscules, de la seva columna seguida del nombre de la seva fila.

• Entreu a la cel·la A1 el número 3.
• Entreu a la cel·la A2 el número 1.

Per entrar cada número cal que acabeu cada vegada amb Retorn.

Aquests dos nombres que heu entrat estan assignats a les variables A1 i A2. Per comprovar-ho, accediu a Visualitza | Objectes auxiliars. Observeu que han aparegut aquestes variables numèriques amb els valors assignats. Així doncs, tots els continguts de les cel·les del full de càlcul es consideren Objectes auxiliars i queden enregistrats en aquest apartat, que podeu fer que sigui visible, o no, de la finestra algebraica.

• A la línia d'entrada escriviu B1=8 i després B2=2 (amb majúscules). Veureu que aquests dos nombres també apareixen a les cel·les corresponents del full de càlcul.

Així doncs, també podeu introduir dades al full de càlcul des de la línia d'entrada.

Observeu que si feu algun canvi a la cel·la A1, per exemple, aquest es reflecteix a la finestra algebraica i al revés. Observeu també que els objectes auxiliars creats tenen davant el símbol que indica que són invisibles.

• Cliqueu sobre el símbol que precedeix la variable A1, per fer-la visible, i observeu què passa.

Com ja havíeu vist en el mòdul 2, aquesta variable numèrica, en fer-se visible, s'ha convertit en un punt lliscant. Aquest fet ens fa pensar que un punt lliscant també es pot entendre com una variable numèrica que s'ha fet visible. Com ja sabeu, aquesta propietat no és exclusiva de les variables generades per les cel·les d'un full de càlcul, sinó que es compleix per a qualsevol.

• Moveu el punt lliscant i observeu.

Ja teniu, doncs una relació molt estreta entre la finestra algebraica, la zona gràfica i el full de càlcul.

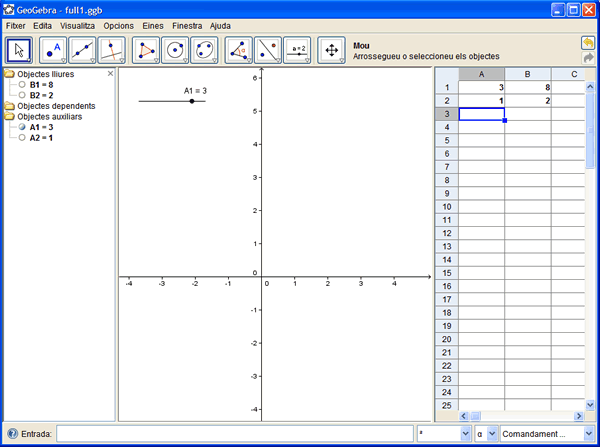
• Seleccioneu les cel·les A1 i A2.
• Situeu el punter del cursor sobre el petit quadrat blau de la part inferior dreta de la zona seleccionada i, amb el botó esquerre del ratolí premut, estireu, tot seguint la columna A, cap a la part inferior; deixeu anar el botó esquerre i observeu.

Efectivament, s'ha creat una progressió aritmètica a partir dels valors numèrics de les cel·les A1 i A2. Observeu que les cel·les afectades també apareixen dins dels Objectes auxiliars.

• Feu que només estigui seleccionada una cel·la qualsevol del full i moveu el punt lliscant A1 corresponent a la cel·la del mateix nom. Veureu com la progressió s'actualitza immediatament.

• Feu un doble clic a la cel·la A1 i veureu que apareix un signe igual davant del nombre. Si feu el mateix a la cel·la A6, o a qualsevol d'aquelles que queden per sota de l'A2, observeu que surt la fórmula que ha fet servir el full de càlcul per calcular els termes de la progressió aritmètica.

Les cel·les del full de càlcul poden contenir altres objectes matemàtics i també textos. Es poden introduir des de la línia d'entrada, o bé directament al full de càlcul.

• Introduïu a la línia d'entrada C1="Hola" (la majúscula del nom de la variable i les cometes són imprescindibles!).
• Introduïu a la cel·la C2 Bon dia! (aquí no calen cometes).

Veureu que a prop de l'origen de coordenades ha sortit el rètol Hola, mentre que l'altre no ha sortit. Per defecte, els textos introduïts a la línia d'entrada per a una cel·la del full de càlcul són visibles i situats a prop del punt (0,0) i els que escrivim directament al full de càlcul són invisibles. Si els feu visibles, també apareixen situats allà mateix. Entrem-hi punts.

• Introduïu a la cel·la D1, directament (2,1). Veureu que aquest punt apareix a la zona gràfica amb el nom de D1 i també consta com a objecte auxiliar. Si el desplaceu, l'actualització de les seves coordenades apareix tant en el full de càlcul com a la finestra algebraica.

• En canvi, si haguéssiu introduït D1=(2,1) des de la línia d'entrada, apareix al full de càlcul i a la finestra algebraica, però com a objecte lliure.

Suposem que encara teniu dades numèriques a les cel·les A2 i B2.

• Entreu a la cel·la D2 (A2,B2). La representació del punt D2 ja es pot veure a la zona gràfica.
• Seleccioneu les cel·les D1 i D2. Estireu el petit quadrat blau, com heu fet abans, cap a la part inferior de la columna i deixeu anar el botó del ratolí.

Al full de càlcul teniu un conjunt de punts, les coordenades dels quals formen una "doble progressió aritmètica" a partir dels punts D1 i D2; a la zona gràfica teniu la seva representació.

• Desplaceu a la zona gràfica els punts D1 i D2 i observeu tots els canvis que es produeixen a les diferents parts de la pantalla: finestra algebraica, zona gràfica i full de càlcul.

Podeu definir objectes matemàtics a les cel·les del full de càlcul. Per exemple:

• Entreu a E2 l'expressió recta[D1,D2] i observeu què passa.

És convenient que aneu fent proves per anar veient les possibles relacions entre finestra algebraica, zona gràfica i full de càlcul a l'hora de definir i manipular els diferents objectes matemàtics.

Hem vist exemples d'ús dels recursos associats al full de càlcul de GeoGebra. En properes pràctiques treballarem a bastament temes d'estadística, però ara volem mostrar una altra utilitat possible del full de càlcul: fer de suport per emmagatzemar diferents objectes que puguin fer-se visibles en funció d'un punt lliscant. Observeu la finestra següent:

Si desplaceu el punt lliscant, veureu que la funció f(x) va agafant cadascuna de les tres expressions que estan situades a les cel·les A1, A2 i A3, segons el seu valor. En conseqüència, la derivada, en vermell, també canvia. Passem a la construcció.

• Entreu a les cel·les A1, A2 i A3 les expressions de tres funcions que veieu a la finestra activa. Si la columna és massa estreta, la podeu ampliar com ho faríeu en altres fulls de càlcul, és a dir situant el punter sobre la frontera entre la columna A i la B, a la part superior del full, i desplaçar-la.
• Creeu el punt lliscant a amb 1 i 3 com a valor mínim i màxim i 1 com a increment.
• Escriviu a la línia d'entrada l'expressió

  f(x) = Objecte["A" + a]

En aquesta expressió esteu fent servir el comandament Objecte["Nom d'un objecte escrit com un text"]. Aquest és un comandament que té una funcionalitat molt especial: si se li entra el nom d'un objecte, escrit com a text, retorna una còpia del mateix objecte i el presenta a la zona gràfica si és un element de dibuix.

Per exemple, en el nostre cas, A1 és el nom assignat a la primera funció, perquè l'heu introduïda precisament a la cel·la A1. Així doncs, si entreu a la línia d'entrades

t(x)=Objecte["A1"]

veureu que la funció t(x) que acabeu de definir té per expressió la mateixa que conté la cel·la A1. Observeu que les cometes són obligatòries, perquè el nom ha de tenir format de text.

Ara bé, el que és realment potent d'aquest comandament és que el nom de l'objecte pot ser dinàmic. Així, si heu escrit

 f(x) = Objecte["A" + a] 

seguint la sintaxi dels textos, us referiu als noms dels objectes A1, A2 o A3, segons el valor que agafa el punt lliscant a.

• A continuació, definiu la derivada g(x) = f'(x).

Acabeu els detalls estètics i deseu la feina!