Punts, vectors, nombres complexos
En l'ajuda del GeoGebra llegim que hi ha dos punts de vista que es mostren paral·lelament: una expressió a la finestra algebraica es correspon amb un objecte a la zona gràfica i a l’inrevés.
Ja hem vist que mentre fem les nostres construccions, tant si tenim els eixos a la vista com si no, podem consultar les equacions i coordenades dels objectes. Això també és així encara que no tinguem a la vista la finestra algebraica perquè, naturalment, el treball intern del programa sempre és analític.
En aquesta pràctica veurem com podem crear els tres tipus d'objectes que s'esmenten en el títol, com podem emprar-los per al nostre treball amb el GeoGebra i com es relacionen entre ells.
Punts
Per crear un punt en la línia d'entrada hem d'escriure'n les coordenades que, com segur que ja imagineu, poden venir donades per punts lliscants o altres variables. Feu-ne proves!
- Si escrivim (3,2) el GeoGebra crearà un punt amb aquestes coordenades i l'anomenarà amb la primera lletra majúscula lliure. Com ja podeu imaginar, aquest punt el podrem moure després interactivament.
- Si m i n són dues variables numèriques donades per punts lliscants podem escriure (m,n) i es crearà un punt les coordenades del qual variaran amb els punts lliscants.
- Si volem crear un punt donant-li nom escriurem, per exemple, M=(4,-1) o bé P=(m,n). Per crear-los, hem de donar als punts un nom que comenci amb una majúscula: M o P com hem indicat, o també Abracadabra o HOLA. Si volem, quan ja estigui creat l'objecte punt, li podrem canviar el nom i posar-n'hi un altre que comenci en minúscula però, per crear-lo, el nom ha de començar en majúscula perquè, altrament, GeoGebra entén que ens referim a un vector.
Per obtenir les coordenades d'un punt tenim les funcions x() i y().
- Si tenim un punt M=(4,-1) aleshores x(M) crea un valor numèric que inicialment té el valor 4; si tenim un punt P=(m,n) aleshores y(P) pren el valor donat per la variable numèrica n.
Aquest recurs permet dissenyar la macro de la pràctica 1 d'aquest mòdul, que serveix per construir un rectangle de costats paral·lels als eixos amb una simplicitat extraordinària.
- Definiu dos punts A i B, els que vulgueu. Podeu fer-ho clicant amb l'eina Punt nou activada o entrant els valors a mà, per exemple A=(-2,1) i B=(3,2).
- Si reflexioneu un moment, veureu de seguida que els altres dos punts que ens interessen per al rectangle ACBD que volem construir han de tenir una coordenada d'un dels dos vèrtexs inicials i l'altra coordenada de l'altre vèrtex. Escriviu doncs C=(x(A), y(B)) i D=(x(B), y(A)) i veureu de seguida que s'han creat els dos punts que volíem.
- Podreu construir el rectangle amb l'eina Polígon o bé amb el comandament Polígon[A,C,B,D].
- Moveu els punts A i B i veureu que tot funciona com interessava. A partir d'aquí ja es crearia la macro com hem explicat en la pràctica 1.
Entre les opcions del GeoGebra hi ha la de mostrar les coordenades polars d'un punt si accedim a Propietats. Vegeu-ho:

- Noteu que directament, amb el botó dret, podem accedir a les coordenades polars del punt. Si obrim la finestra de propietats, a més, podem reconvertir el punt en un objecte nou, un nombre complex. D'això en parlarem més endavant en aquesta pràctica.
- La coordenada angular es mostra en l'interval [0º, 360º] si treballem en graus, o bé en [0, π] ∪ [-π, 0] si treballem en radiants (en aquest cas es veu positiva per als dos primers quadrants i negativa per al tercer i el quart).
- Podem mostrar alguns punts en coordenades polars i d'altres en coordenades cartesianes. Això és una propietat de cada punt. Però si treballem en coordenades polars, per tots els punts (o vectors, o nombres complexos que veurem després) ho hem de fer en graus o per tots els punts en radiants.
- En la versió de GeoGebra del moment en què es redacta aquesta pràctica no hi ha cap funció per recuperar per separat la coordenada radial i la coordenada angular. Però ben segur que en futures versions això sí que serà possible.
- Es pot crear un punt en coordenades polars. Per fer-ho cal escriure-ho tal com ens el mostra el programa: (coordenada radial; coordenada angular), amb molt de compte amb el signe de punt i coma.
Experimenteu i ja sabeu, que si cal, podeu preguntar a l'entorn de tutoria del curs o, encara millor, posar-ho en comú en el Fòrum.
Vectors
Ja hem comentat en l'apartat anterior que hi havia característiques comunes en la creació de punts i vectors. Ara ho detallem.
- Si volem crear un vector des de la línia d'entrada caldrà donar-li un nom, que haurà de començar amb una lletra minúscula. Per exemple u=(4,-1) o bé vector=(m,n) essent m, n punts lliscants
- Els vectors creats des de la línia d'entrada es dibuixen amb origen en el punt (0,0).
- Això ho podem canviar movent el vector a mà, paral·lelament. Amb compte, perquè si movem justament el punt extrem del vector, aleshores en canviem els components.
- També podem accedir a la finestra de propietats del vector i obrir la pestanya Posició, que ens permet dir en quin punt volem l'origen del vector. Amb compte, també, perquè si hem fet això i intentem moure el vector a mà en varien els components.
- També podem crear vectors amb l'eina Vector entre dos punts, prou explicativa.
- Quan ja tenim un vector creat en podem mostrar diversos representants amb l'opció Vector des d'un punt (equipol·lent a un altre).
Naturalment el GeoGebra té incorporades les operacions amb vectors i la representació gràfica ens ajuda a fer-les visuals.
La imatge següent mostra uns vectors u i v i la combinació lineal 1.5u+1.8v juntament amb elements auxiliars que ajuden a veure com s'ha fet l'operació.
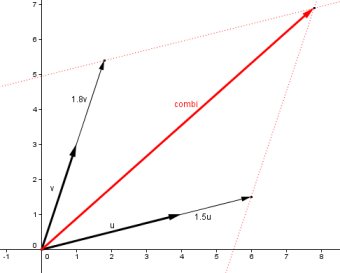
Com s'ha fet la construcció? Com que una imatge val més que mil paraules, teniu tot seguit la reproducció de la finestra que s'obté amb Visualitza | Passos de la construcció.
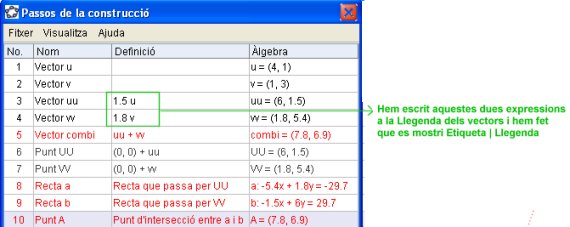
- Recordeu que, tot i que els vectors u i v s'han definit amb uns components fixos, els podeu moure interactivament i observar. En un exercici us demanarem que milloreu la construcció fent servir punts lliscants a i b per dibuixar la combinació lineal a*u+b*v
- Adoneu-vos que GeoGebra incorpora la idea clau de punt + vector = punt a partir de la identificació entre un punt i el seu vector de posició. El comandament Vector[punt] construeix el vector de posició del punt, però no hi ha un comandament que ens doni el punt extrem d'un vector u que podem obtenir, això sí, fent (0,0) + u.
- Com exemple del treball de la geometria afí que acabem de comentar vegeu com de senzill és trobar el quart punt d'un paral·lelogram ABCD del qual en coneixem tres vèrtexs, A, B i C.
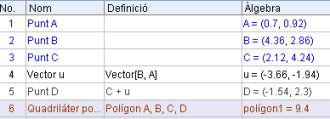
- Tal com ja hem dit per als punts, també podem mostrar els vectors en coordenades polars i reconvertir-los en nombres complexos, del quals en parlem tot seguit. Teniu un comandament que dóna la longitud 1) d'un vector, Longitud[v] però, com ja hem dit, de moment no en tenim cap que doni directament l'argument.
- Els signes u*v o u v amb un espai serveixen per obtenir producte escalar dels vectors u i v. Aleshores, si voleu comprovar la "fórmula del cosinus" que empra el nostre alumnat de Batxillerat per calcular l'angle entre dos vectors u i v, podeu escriure cos(Angle[u,v]) i veure que el resultat és el mateix que el de u*v/(Longitud[u]*Longitud[v]).2)
Nombres complexos
La versió 3.2 del GeoGebra ha incorporat com a novetat la creació d'un objecte nou Nombre complex i és possible entrar l'expressió binòmica de nombres complexos, operar-hi, i, a més fer càlculs i visualitzar-los.
- Podeu obrir un fitxer nou de GeoGebra; treballarem amb els eixos i la graella visibles.
- Per treballar amb els nombres complexos a = 2 + 3i i b = 4 + i, escriviu directament les dues expressions anteriors en la línia d'entrada. Veureu que s'han escrit els dos nombres complexos en la finestra algebraica i que s'han dibuixat dos punts que corresponen als afixos d'aquests nombres complexos. 3) Si accediu al quadre de diàleg de Propietats, veureu això:

- Adoneu-vos que hi tenim tres nombres complexos, a, b i la unitat imaginària i que s'ha creat automàticament com objecte auxiliar. Això no seria possible si abans de la nostra entrada de nombres complexos en forma binòmica hagués existit un objecte definit amb l'identificador i.
- Si resulta que, com la majoria de la gent que coneixem, sou partidaris de mostrar visualment els nombres complexos mitjançant un vector d'origen en l'origen de coordenades i extrem en l'afix del nombre complex, bastarà que definiu Vector[a] i Vector[b] en la línia d'entrada donant-los el nom que us sembli adequat.4)
- Les funcions x( ) i y( ), que ja coneixem, si els passem com a argument un nombre complex ens donen respectivament la part real i la part imaginària d'aquest nombre complex.
El GeoGebra permet fer operacions amb nombres complexos.
- Escriviu ara a la casella d'entrada s = a + b i tindreu a la vista la suma s que podeu fer mostrar després com un vector si us interessa.
- També es poden fer immediatament totes les combinacions lineals entre nombres complexos. Proveu, per exemple, c = -1.2a + 0.8b. Aneu variant a mà els valors de a i b i observeu.
- Moveu els nombres complexos perquè siguin, per exemple, a=1+2i, b=2-i. Ara escriviu p=a*b (o bé p=a b si us agrada això que un espai en blanc vulgui dir producte) i observeu.
Més avall comentem com es pot accedir a fer visual el mòdul i l'argument d'un nombre complex i aleshores ja estareu a punt de fer l'exercici que us demanem per mostrar la propietat que diu que el resultat de multiplicar dos nombres complexos és el que té per mòdul el producte dels mòduls dels factors i per argument, la suma dels arguments.
- Finalment, escriviu u = a/b i vegeu que es fa el càlcul de la divisió de nombres complexos. Tanmateix, per defecte, el resultat no es dóna amb fraccions (com segurament ens agradaria) sinó amb decimals.5)
- De moment (suposem que a l'espera de la inclusió en el GeoGebra d'un calculador simbòlic) no tenim incorporat automàticament el càlcul d'arrels de nombres complexos. En parlarem en el mòdul següent com a exemple de l'aplicació de llistes i seqüències.
Per acabar aquesta pràctica farem una referència al treball dels nombres complexos en forma polar.
Mireu aquesta activitat:
- Si obrim el quadre de diàleg de Propietats i per a un nombre complex accedim a Àlgebra | coordenades polars tindrem a la vista la seva forma polar (dita de vegades trigonomètrica) que es mostra així:
(mòdul;argument). - Si volem tenir a la vista la forma binòmica i la forma polar (i també per altres raons) convé definir el vector associat al nombre complex i fer que sigui aquest el que es mostri en forma polar.
- Si volem entrar un nombre complex en forma polar escriurem en la línia d'entrada, per exemple, (4; 32º), i aleshores convertirem el punt o el vector que s'hagin creat a nombre complex. Immediatament en veurem la forma binòmica en la finestra algebraica.
- Com hem fet en altres moments d'aquesta pràctica, recordem la possiblitat de mostrar els passos de cada construcció i també indiquem d'aquesta manera com s'ha elaborat l'activitat GeoGebra amb la qual acabeu de treballar. La imatge següent compara els passos de la construcció tal com els indica GeoGebra i mostra què hem d'escriure en la línia d'entrada.
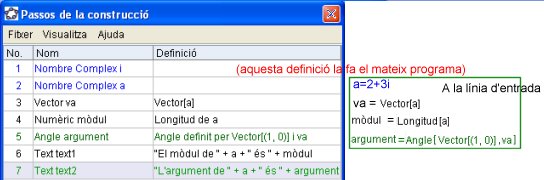
FórmulaText[x(u)]+"+"+FórmulaText[y(u)]+" i"Però aquest comandament només ens permet "escriure bonic" el resultat; no serveix per a operar-hi.

